Цели. Сформировать у детей представления о существенных признаках прямоугольника и квадрата, ориентируясь на которые, они могли бы распознать эти фигуры; развивать умения наблюдать и сравнивать.

Оборудование. Индивидуальные доски для отвечающих у доски учеников; комплекты геометрических фигур для всего класса; угольники; рисунки геометрических фигур для иллюстрирования геометрической сказки.

ХОД УРОКА

I. Организационный момент

II. Мобилизующий этап

Учитель. Посмотрите на чертеж на доске.

На доске:

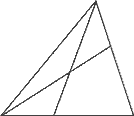
 – Какие фигуры вы нашли?

Дети. Треугольники и четырехугольник.

Дети выходят к доске и показывают найденные фигуры на чертеже.

У. Дайте определение треугольника.

Д. Геометрическая фигура, у которой три стороны, три угла, три вершины.

У. Сколько на чертеже треугольников?

Д. Восемь.

У. Молодцы. Сегодня на уроке нас ожидает встреча с удивительной наукой – геометрией.
Слово геометрия в переводе с греческого языка означает "измерение Земли" (geo – Земля, metrio – мерить).
Но сначала настроимся на урок, так как задания, которые я вам предложу, требуют внимания, дисциплины, знания математической терминологии, свойств и законов и быстрых вычислительных навыков.

III. Арифметический диктант

Дети записывают ответы в тетрадь. Два ученика работают на индивидуальных досках для дальнейшей проверки работы.

У. Запишите число, которое больше 36 и меньше 38.
Первое слагаемое – 8. Второе слагаемое неизвестно. Значение суммы равно 15.
Уменьшаемое неизвестно, вычитаемое – 5, значение разности – 65. Чему равно уменьшаемое?
Задуманное число увеличили на 13 и получили 36.
Это число, в котором 8 десятков, а единиц на 4 меньше.
Число, предшествующее числу 60, уменьшили на 0. Какое это число?
К сумме чисел 9 и 5 прибавили 30.
На сколько 80 больше 7?
Проверим, что у вас получилось.

Дети открывают ответы на досках.

– Какое из этих чисел лишнее? Почему?

Д. 7 – однозначное.
– 70 – круглое.

У. На какие группы можно разбить эти числа?

Д. На однозначные и двузначные.
– На круглые и некруглые.

IV. Практическая работа

У. Возьмите каждый фигуру, которая лежит на подносе. Что это за фигура?

Д. Треугольник.

У. Подумайте, как из него получить квадрат.

Дети делят фигуру, как показано на рисунке, затем соединяют детали. Учитель повторяет правила безопасности при работе с ножницами.

– Вы получили квадрат. Расскажите о нем.

Д. У квадрата четыре вершины, четыре стороны, четыре угла.

У. Что можно сказать об углах?

Д. Они прямые.

При помощи угольников или модели прямого угла выясняется, что углы у квадрата прямые.

У. Возьмите в руки линейки, измерьте стороны квадрата.

Д. Все стороны равны.

У. Сколько углов и сторон у квадрата?

Д. По четыре.

У. Четное количество углов, сторон. Как можно назвать квадрат по-другому?

Д. Четырехугольник.

Учитель на доске фиксирует свойства квадрата.

У. Рассмотрите рисунки на доске.

На доске:

– Из каких геометрических фигур составлен первый рисунок?

Д. Квадрат, два треугольника, круг.

У. Какая фигура лишняя?

Д. Круг, так как он не имеет углов.

У. Из каких геометрических фигур составлен второй рисунок?

Д. Прямоугольник, три треугольника, круг.

У. Чем отличаются рисунки?

Д. Количеством треугольников и тем, что на первом рисунке – квадрат, а на втором – прямоугольник.

У. О какой еще фигуре мы будем говорить?

Д. О прямоугольнике.

V. Физкультминутка

VI. Знакомство с новым материалом

У. Я расскажу вам сказку. Она необычная, математическая и называется "Родственники".

Жила на свете важная фигура. Важность ее признавалась всеми людьми, так как при изготовлении многих вещей форма ее служила образцом. Кого бы ни встретила она на своем пути, всем хвалилась: "Посмотрите, какой у меня красивый вид: стороны мои все равны, углы все прямые. Красивее меня нет фигуры на свете!"

Учитель показывает рисунок.

– Назовите эту фигуру, ребята!

Д. Квадрат.

У. Как вы узнали?

Д. Стороны равны, углы прямые.

У. Ходил Квадрат по свету, и стало тяготить его одиночество: не с кем побеседовать и потрудиться в хорошей и дружной компании. Ведь весело и легко бывает только с друзьями. И решил Квадрат поискать родственников... "Если встречу родственника, то сразу его узнаю, – думал Квадрат, – ведь он должен быть похож на меня".
Однажды встречает он на пути такую фигуру:

Пригляделся Квадрат к ней и увидел что-то знакомое. "Как тебя зовут?" – спрашивает.
Узнали, дети?

Д. Это прямоугольник.

У. Почему он так называется?

Д. У него все углы прямые.

Осуществляется проверка у доски.

У. Давайте измерим длину сторон. Что вы о них скажете?

Д. Стороны, которые лежат одна против другой, равны.

Учитель на доске фиксирует свойства прямоугольника.

У. Называются эти стороны противоположными. Сформулируйте вывод о противоположных сторонах прямоугольника.

Д. Противоположные стороны прямоугольника равны.

У детей на партах по два прямоугольника разного цвета. Длина красного прямоугольника больше длины синего, а ширина одинакова.

У. В этом можно также убедиться, не измеряя стороны по линейке. Предложите такой способ.

Д. Наложением.

У. Накладываем одну фигуру на другую и замечаем, что противоположные стороны равны.

В чем же отличие квадрата от прямоугольника?

Д. У квадрата все стороны равны, а у прямоугольника – только противоположные.

У. У прямоугольника та сторона, которая длиннее, называется "длина". Сторона, которая короче, называется "ширина".
Сравните красный и синий прямоугольники, используя понятия "длина стороны" и "ширина стороны".
Как определить, где у квадрата длина, а где ширина?

Д. У квадрата все стороны одинаковой длины.

VII. Закрепление нового материала

У. Давайте поучимся чертить прямоугольник, используя свойства сторон. Начертите прямоугольник, длина которого – 5 сантиметров, а ширина – 3 сантиметра. Как можно их расположить?

На доске:

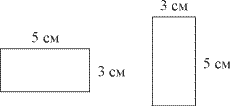
– Подумайте, можно ли из этого прямоугольника получить квадрат?

Д. Взять за сторону квадрата ширину или длину прямоугольника.

У. Начертите в тетради квадрат любым способом.

Дети выполняют задание.

– Кто начертил квадрат со стороной 3 сантиметра, кто – со стороной 5 сантиметров?
А теперь послушайте продолжение сказки.
Квадрат спрашивает у Прямоугольника:
– А мы не родственники с тобой?
– Я бы тоже был рад узнать об этом, – говорит Прямоугольник. – Если у нас найдется четыре признака, по которым мы похожи, значит, мы с тобой близкие родственники и у нас может быть одна фамилия.
Давайте поможем фигурам найти такие признаки, обобщим полученные знания.

Д. У фигур четыре угла, все фигуры прямые, у них по четыре стороны, противоположные стороны равны.

У. А какая же у них общая фамилия?

Д. Прямоугольники.

У. Обрадовались фигуры, что нашли друг друга. Отдыхают вместе, трудятся. Один раз гуляли на полянке, и прямо к ним направляется фигура, имеющая такой вид:

Вежливо поздоровавшись, говорит: "Долго я искал представителей нашего старинного рода. Наконец-то я нашел своих близких родственников!"
– А как же тебя зовут?
– Четырехугольник.
– Как же доказать, что мы твои родственники?
– Мы имеем два общих признака.
Они были названы.
А вы, ребята, сможете их назвать?

Д. Четыре угла, четыре стороны.

У. Так встретились и жили одной дружной семьей три родственные фигуры, которые назывались четырехугольники.

К концу урока на доске появляется таблица:

VIII. Итог урока

У. Какие утверждения правильны?

На доске:

Д. Правильные – первое и третье утверждения.

У. Завтра, ребята, мы продолжим разговор о многоугольниках.
Спасибо за хорошую работу!