Цели. Подвести детей к понятию округления чисел с точностью до сотен; продолжить работу над преобразованием задач; формировать устные и письменные вычислительные навыки.

Оборудование. Учебник "Математика. 4-й класс" (сост. И.И. Аргинская, Е.И. Ивановская). Самара: Изд-во "Учебная литература" "Корпорации "Федоров", 2001).

ХОД УРОКА

I. Организационный момент

Учитель. Сегодня работу на уроке мы построим по такому плану:

– продолжим работу с приближенными числами;
– решим задачу;
– узнаем что-то новое об округлении чисел;
– поработаем с произведениями.

План записан на доске, дети читают его самостоятельно, после чего план закрывается.

II. Актуализация знаний учащихся

У. Какое у вас было домашнее задание?

Дети. Надо было округлить разными способами с точностью до десятков числа 381, 1754,
90 786, 7 562 и подчеркнуть тот способ, который лучше.

У. Сравните свои записи с записями на доске.

На доске:

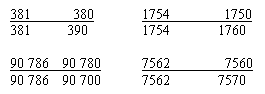
Д. При округлении числа 1754 на доске неправильно был подчеркнут вариант. Если заменить это число 1760, ошибка будет 6, а если взять 1750 – ошибка 4. Это лучше – ведь 4 < 6.
– На доске еще есть ошибка – не должно быть записи: 90 786 90 700.
– Когда округляли до десятков, мы находили такое число, чтобы разница была меньше десяти, а здесь разница 86 – это больше десяти.
– Здесь нужно взять число 90 790.
– И тогда лучше будет округлить 90 786 до 90 790.
– Когда мы округляем до десятков, то нули появляются только в разряде единиц, а здесь они и в разряде единиц, и в разряде десятков.
– А мне кажется, что иногда и при округлении до десятков могут получиться нули в разряде десятков. Вот, например, 597 с точностью до десятков лучше всего округлить до 600.
– Правильно, я думаю, если число оканчивается больше чем на 95, так будет всегда получаться. Но число 90 786 кончается меньшим числом, и так получиться не может.
– Мне кажется, что число 90 786 тоже округлили, только с другой точностью.

III. Изучение нового материала

У. Что вы можете сказать об этой паре чисел: 90 786 и 90 700?

Д.  Я думаю, если в приближенном числе нули стоят в разрядах десятков и единиц, то чаще всего это значит, что мы его округлили до сотен.
– Мне кажется, что это и есть наше новое знание – числа можно округлять не только до десятков, но и до сотен.
– А я думаю, что это знание помогает предположить, что числа можно округлять с любой точностью.

У. Вы согласны с ребятами?

Дети соглашаются и объясняют это.

– Что значит округлить число с точностью до сотен?

Д. Я думаю, что это значит вместо десятков и единиц написать нули.
– Мне кажется, это неточно, надо еще посмотреть, какая цифра должна быть в сотнях.

У. Найдите и прочитайте в учебнике задание 161, пункт 3.

– Верен ли ответ: округлить число с точностью до сотен – это значит заменить его одним из ближайших чисел, у которых в разрядах единиц и десятков нули?

Д. Мне кажется, что здесь все правильно.
– А я думаю, что здесь есть неточность – ведь ничего не говорится об изменении разряда сотен.
– Нет, ты не права: посмотри, здесь есть слова "одним из ближайших чисел", а они и будут отличаться цифрой в сотнях.
– Да, здесь все правильно сказано.

У. Выполните самостоятельно пункт 5 этого же задания.

Дети быстро и без затруднений выполняют задание, после чего проводится проверка: ученики называют разницу между точным и приближенным числами.

– Посмотрите пункт 7 этого задания.

Д. Первое число округлили с точностью до сотен – ведь нули поставили в разряде десятков и разряде единиц.
– Число 168 294 округлили до десятков тысяч – ведь значащие цифры есть только в разрядах сотен и десятков тысяч.
– Последнее число округлили до сотен тысяч.
– А мне кажется, что в последнем числе может быть и округление до десятков тысяч. Здесь такой случай.
– Я понял: числа можно округлять с разной точностью.
– Правильно, это зависит от того, сколько разрядов в числе.

У. Посмотрите, что записано на доске.

На доске:

– Это произведения.

– Можно сказать так: выражения с действиями второй ступени.

У. Что вы можете о них сказать?

Д. В них двузначное число умножают на двузначное.
– Первый множитель везде равен 83.
– Есть "лишнее" произведение 83 х 53, в остальных во втором множителе 4 десятка.
– Их можно разделить на группы, где значения будут четными (83 х 46 и 83 х 42), а в остальных значения будут нечетными.

У. Запишите произведения в порядке убывания, не выполняя действий.

Дети самостоятельно делают записи в тетрадях.

– Что помогло выполнить задание?

Д. То, что первые множители одинаковые, а вторые меняются. Чем он меньше, тем меньше значение произведения.

У. Найдите значения произведений.

Дети самостоятельно выполняют умножение.

– Проверьте свою работу.

Открывается запись на доске.

Все ученики выполнили работу без ошибок.

– Что вы заметили?

Д. Значения произведений тоже убывают.

– Но разница между соседними значениями не одинаковая.

У. На сколько каждое следующее значение произведения меньше предыдущего?

Д. В произведениях: 83 х 47, 83 х 46, 83 х 45 значения уменьшаются на 83, потому что первый множитель 83, а вторые уменьшаются на 1.
– 83 х 53 меньше 83 х 49 на 332, так как 4399 – 4067 = 332.
– А можно было 83 х 4 = 332, ведь мы берем по 83 на 4 раза меньше.
– 83 х 47 меньше 83 х 49 на 166.
– 83 х 42 меньше 83 х 45 на 249.

У. Подумайте, что надо сделать, чтобы разница между значениями произведений стала одинаковой?

Д. Можно зачеркнуть произведения 83 х 47, 83 х 46 и 83 х 42, тогда разница везде станет 332.
– Можно добавить произведение 83 х 49, а 83 х 46 и 83 х 42 вычеркнуть, тогда разница станет 166.
– Можно добавить несколько произведений, тогда разница еще уменьшится.

У. Выполните самостоятельно задание № 163, пункты 3 и 4.

Какие произведения нужно добавить, чтобы разница стала одинаковой? Запишите такие произведения, покажите их место и найдите их значения.

Задание выполняется самостоятельно, затем проверка.

Д. Надо добавить произведения:

– Теперь разница везде равна 83 – ведь первые множители не изменяются, а вторые множители уменьшаются на 1.

У. Молодцы, это задание вы выполнили без затруднений и ошибок. Теперь будем работать с заданием № 162, пункт 1. Решите задачу.

Д. Нам надо решить составную задачу.
– Можно ее решать самостоятельно?

У. Конечно. Кому потребуется помощь, поднимите руку.

Одна ученица выполняет задание на откидной доске.

На доске:

У. Измените условие задачи так, чтобы ее решение стало короче. Запишите задачу.

Дети записывают свои задачи в тетрадях.
В результате появляется два варианта.

– Рома, ты какую составил задачу?

Рома. В ларек и магазин привезли на восьми машинах 32 т овощей. В магазин привезли 24 т, а остальные в ларек. Сколько машин привезли овощи в магазин и сколько в ларек?

У. Давайте решим эту задачу.

На доске:

У. А ты, Маша, какую задачу составила?

Маша. В ларек и магазин на 8 одинаковых машинах привезли овощи. В магазин привезли 24 т, а в ларек – 8 т. Сколько машин привезли овощи в ларек и сколько в магазин?

У. Решите Машину задачу.

Дети решают в тетрадях, один ученик у доски.

На доске:

У. У кого-нибудь есть другие варианты?

Других вариантов нет.

– Как еще вы можете предложить преобразовать задачу?

Д. Можно так изменить условие, чтобы получилась задача с лишними или недостающими данными. Но такого задания не было.
– Можно изменить вопрос, чтобы задача решалась меньшим количеством действий.
– Можно так изменить задачу, чтобы действий стало больше.

IV. Домашнее задание

У. Вот это и будет одним из ваших домашних заданий. Запишите домашнее задание: № 162, пункты 3, 4 (по выбору); со значениями произведений из № 163 составить суммы, в которых при вычислении будет переход в разрядах единиц, десятков и сотен.

V. Подведение итогов урока

У. Наш урок подошел к концу. Что вы о нем можете сказать?

Д. Я думаю, урок был интересным и полезным.
– На нем нужно было много думать.
– Мне урок очень понравился: мы еще больше узнали об округлении чисел, много всего успели сделать, весь план выполнили.
– А я хочу сказать, что мы работали совсем не по плану, который был написан на доске. Это, наверно, не так уж важно, но все-таки если есть план, его нужно стараться выполнять.

У. Это очень интересное наблюдение. Кто-нибудь еще заметил отступление от плана?

Д. Да, мы тоже это заметили (ответ многих детей).
– Мне кажется, что план урока был такой:

1. Работа с домашним заданием.
2. Продолжение изучения округления чисел.
3. Работа с произведениями.
4. Решение задачи и ее преобразование.

– А я думаю, что не стоит отдельно выделять работу с домашним заданием: она относится к округлению чисел.

У. Все согласны с ребятами?

Все согласны с последним вариантом плана урока.

– Молодцы, спасибо за хорошую работу на уроке.