Первое открытие всегда заключается в том,
что есть вещи, которые стоит открывать.
Д. Томсон. «Дух науки»
Оборудование.
- Карточки с заданиями для каждой команды.
- Компьютер, проектор, экран, презентация.
Время. 150 минут.
Цель мероприятия:
- Используя занимательную игру, развивать и укреплять
познавательный интерес к предмету математики, воспитывать культуру
математического мышления.
Задачи мероприятия:
- развивать логическое мышление, речь;
- развивать умение применять знания в новой ситуации;
- развивать исследовательские навыки;
- расширять познавательную свободу ученика;
- развивать умение работать в группе, отстаивать свое решение;
- способствовать раскрытию творческого потенциала учеников.
Ученики 5-6 классов, интересующиеся математикой, принимают участие
лишь в школьном этапе Всероссийской олимпиады школьников. Но им для
реализации своих способностей этого недостаточно. Поэтому ученики 5-6
классов с удовольствием принимают участие во всех внеклассных
мероприятиях, тем более в таком традиционном мероприятии, как
математическая викторина. Данная викторина рассчитана на учеников 5
классов, обучающихся по УМК Дорофеева Г.В. , Петерсон Л.Г.
Правила игры: Викторина проводится в лицее в рамках
недели математики (февраль). В игре принимают участие команды учеников
5-х классов (от каждого класса по 6 участников). Например, в н лицее -
шесть пятых классов, то есть участвуют 6 команд. Каждая команда
выбирает себе название, девиз, эмблему, капитана. В игре задействованы
еще 9 учащихся старших (7 или 8) физико-математических классов, которые
выступают в роли экспертов (жюри). Командам заранее предлагается
домашнее задание, которое они решают всей командой в классе в течение
45 минут (например, после уроков). Решенные домашние задания собирает
учитель и передает для проверки жюри. Члены жюри, предварительно решают
самостоятельно все задания викторины. Затем члены жюри оценивают
решенные домашние задания и присуждают каждой команде первые баллы.
При этом ученики старших классов не только повторяют ранее изученный
материал, но и затем в ходе викторины могут прокомментировать
представленные решения команд.
Также от каждой команды готовится сообщение на 2-3 минуты из истории
математики, математический фольклор и т.д. Сообщения красочно
оформляются на листе формата А 4 .
Во время игры за каждой командой закреплен 1 эксперт,
он проверяет решения и ведет подсчет баллов. Еще 1 член жюри заполняет
протокол викторины, а другой следит за дисциплиной и один ученик
находится за компьютером, помогая провести презентацию.
Также за правильностью хода игры наблюдают преподаватели лицея.
Домашнее задание. (Всего 9 баллов).
- (3 балла). Если к некоторому двузначному числу приписать
справа цифру 0, то это число увеличится на 252. Найти это
двузначное число.
- (3 балла). Три человека хотят поделить между собой 7 полных
бочек, заполненных медом, 7 бочек, заполненных медом наполовину и 7
пустых, но так, чтобы и мед и тара были поделены поровну. Как
произвести этот раздел, не перекладывая мед из одной бочки в
другую?
- (3 балла). Можно ли выбрать из таблицы 5 чисел, сумма которых равна 20?
Решения. (Показ презентации, слайды 3-5, приложение 1)
1. Пусть х – искомое двузначное число. Приписать справа к числу цифру 0 равносильно умножению этого числа на 10, тогда:
10х = х + 252,
10х – х = х + 252 – х,
9х = 252,
х = 28.
Ответ: 28.
2. I способ: первый человек (как и второй) должен взять три полных
бочки, одну полупустую и три пустых; третий – одну полную, пять
полупустых, одну пустую.
II способ: первый человек (как и второй) – две полных бочки, три
полупустых и две пустые; третий – три полных, одну полупустую и три
пустых.
3. Нет, так как сумма пяти нечетных чисел является числом нечетным.
Ход игры
Ведущий: Сегодня мы собрались на математическую викторину «Ключ к победе».
Викторина будет состоять из пяти туров:
- 1 тур – «Математическая эстафета», в котором вас ждут 3 забега.
Каждый забег может принести команде 5 баллов, по количеству правильно
решенных задач. Всего, таким образом, 1 тур может принести команде 15
баллов. Когда к финишу приходит какая-либо команда (или 30 минут), тур
считается законченным.
- 2 тур называется «С миру по нитке». Каждому игроку команды будет
предложено по одной задаче. На решение дается определенное время
(10мин). Максимальное число баллов-6.
- 3 тур – Лингвистический. Максимальное число баллов не фиксируется.
- 4 тур - Геометрический. 2 задачи: первая- 3 балла, а вторая- 5 баллов.
- 5 тур - Финальный. Проводится в том случае, если нельзя выявить
или победителя или призера. Предлагается всего одна задача- 5баллов.
За каждым столиком – великолепная шестерка!
Теперь давайте познакомимся с каждой командой. Каждая команда
представляет название, эмблему девиз. Далее слово предоставляется жюри.
Оно разберет домашнюю работу и назовет первые результаты. Итак,
начинаем наш первый конкурс.
1 тур. Математическая эстафета.
Задача 1. (1 балл) Руслан и Людмила. «Идет направо —
песнь заводит, налево — сказку говорит». Чтобы рассказать сказку,
ученому Коту требуется 5 минут, а чтобы спеть песню — 4 минуты. В
десять часов утра Кот начал рассказывать сказку. Куда будет идти Кот в
полдень?
Решение.
Чтобы рассказать сказку и спеть песню ученому Коту требуется
4 + 5 = 9 мин. За 2 часа с 10 утра до полудня пройдет 120 мин.
120 = 9 · 13 + 3. Значит, за это время Кот успеет спеть 13 песен,
рассказать 13 сказок, и у него останется 3 мин на то, чтобы начать (но
не успеть кончить), рассказывать сказку. А это значит, что в полдень
Кот будет идти налево.
2. (1 балл) В вазе на столе у Мальвины стоит букет
из 7-ми белых и голубых веток сирени. Известно, что 1) по крайней мере,
одна ветка белая, 2) из любых двух веток хотя бы одна — голубая.
Сколько в букете белых веток и сколько голубых?
Ответ: 1 белая ветка и 6 голубых веток сирени.
3. (1 балл) Все считали, что Дракон был однооким,
двуухим, треххвостым, четырехлапым и пятииглым. На самом деле, только
четыре из этих определений выстраиваются в определенную закономерность,
а одно — лишнее. Какое?
Решение.
Лишнее определение — четырехлапый. Во всех остальных определениях в
середине слова есть удвоенные буквы. Кстати, обратите внимание, в
русском языке довольно редко встречаются слова с такими удвоенными
буквами.
4. (1 балл) Продолжите последовательность: 2, 6, 12, 20, 30, …
Решение:
2; 2 + (2 + 2); 6 + (4 + 2); 12 + (6 + 2); 20 + (8 + 2);
Ответ: 30 + 12 = 42, 42 + 14 = 56.
5. (1 балл) Лифт поднимается с первого этажа на третий за 6 секунд. За сколько секунд он поднимается с первого этажа на пятый?
Ответ: 12 секунд.
6. (1 балл) Высота столба 20 метров. Гусеница
ползет по нему, при этом за день она поднимается на 5 метров, а за ночь
опускается на 4 метра . За какое время она доползет до вершины столба?
Решение.
Обычный ответ: за 20 дней, но… Так как за сутки гусеница поднимается
на 1 метр, следовательно за 15 суток она поднимется на 15 метров, а за
шестнадцатый день еще на 5 метров и достигнет вершины столба.
Ответ: 15 суток и один день.
7. (1 балл) Расставьте по кругу четыре единицы, три
двойки и три тройки так, чтобы сумма любых трех подряд стоящих чисел
не делилась на 3.
Ответ: 1, 3, 3, 2, 2, 1, 2, 1, 1, 3.
8. (1 балл) Две куклы из театра Карабаса -Барабаса
играли на гитарах, а одна на балалайке. На чем играл Пьеро, если
Мальвина с Арлекином и Арлекин с Пьеро играли на разных инструментах.
Ответ: Пьеро играл на гитаре.
9. (1 балл) Книга в переплете стоит 64 коп. Сколько стоит переплет книги, если известно, что сама книга дороже ее переплета на 60 коп.?
Решение:
Пусть x- цена переплета, тогда x+60 - цена книги. Составим уравнение x + x + 60 = 64, 2x = 4, x = 2.
Ответ: 2 коп.
10. (1 балл) В харчевне «Трех пескарей» пекут
пирожки и продают их на рынке. В первый день продали 100 пирожков по
цене 1 рубль за один пирожок. На следующий день снизили цену на 10 % и
продали 110 пирожков. В какой день хозяин харчевни заработал больше и
на сколько?
Ответ: в первый день на 1 рубль.
11.
(1 балл) Какая тыква тяжелее?
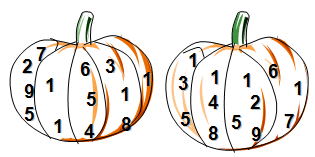
Вес тыквы – это сумма чисел. Но ваша задача: ответить на наш вопрос, не складывая числа. Сумеете?
Ответ: тыква слева тяжелее.
12. (1 балл) Сколько нулей в конце записи числа, выражающего произведение
1 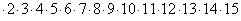 . .
Ответ: 3 нуля.
13. (1 балл) У двух человек было два квадратных
торта. Каждый сделал на своем торте по 2 прямолинейных разреза от края
до края. При этом у одного получилось три куска, а у другого — четыре.
Как это могло быть?
Решение.
Это могло получиться, если в первом случае разрезы не пересекались, а во втором — пересеклись.
14. (1 балл) Печатающее устройство «зациклилось» и
теперь печатает подряд цифры в такой последовательности: 1, 2, 3, 4, 5,
4, 3, 2, 1, 1, 2, 3, 4, 5, 4, 3, 2, 1,… и так далее. Какую цифру оно
напечатает на 2010 месте?
Ответ: 3.
15. (1 балл) Винни-Пух пошел в гости к Пятачку.
Помогите Винни-Пуху найти кратчайший путь от своего дома "А" до дома
Пятачка "К". Числа обозначают время движения (в минутах) от пункта до
пункта. Перечислите пункты, через которые пойдет Винни-Пух и
подсчитайте время, которое он затратит на весь путь.
Ответ: А-Б-Е-Д-З-К, 60 минут.
Во время проверки решений, для участников-показ презентации.
2 тур. С миру по нитке.
1. (1 балл) Найдите все дроби со знаменателем 15, которые больше 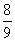 и меньше 1. и меньше 1.
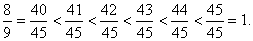
Ответ: 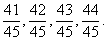
2. (1 балл) Конфеты «Сладкая математика» продаются
по 12 штук в коробке, а конфеты «Геометрия с орехами» – по 15 штук в
коробке. Какое наименьшее число коробок конфет того и другого сорта
необходимо купить, чтобы тех и других конфет было поровну?
Решение:
НОК(12;15) = 60, тогда необходимо 5 коробок с конфетами «Сладкая математика» и 4 коробки с конфетами «Геометрия с орехами».
3. (1 балл) В 22 часа из Ромашково вышел паровозик
со скоростью 50 км в час, чтобы встретить рассвет. Через час за ним
вышел другой паровозик. В 4 часа утра он догнал первый паровозик из
Ромашково. С какой скоростью ехал второй паровозик?
Ответ: 60 (км/ч)
4. (1 балл) С одной станции одновременно в
противоположных направлениях вышли поезд «Стрела» и поезд «Сапсан».
Скорость «Стрелы» 200 км/ч, а скорость «Сапсана» 250 км/ч. Через
сколько часов после начала движения расстояние между поездами станет
1800 километров?
Ответ: 4 часа.
5. (1 балл) Карабас-Барабас погнался за петухом, на
котором сидел Буратино. Петух делает в минуту 300 шагов, каждый шаг 40
см. Карабас-Барабас бежит со скоростью 1 м/с. Догонит ли он петуха с
Буратино?
Ответ: Конечно, не догонит.
6. (1 балл) Расстояние между домами в Цветочном
городке 3 км. Незнайка проходит это расстояние за полчаса, а поэт
Цветик за 1 час. Однажды они договорились встретиться. Незнайка и
Цветик одновременно вышли из своих домиков. Через какое время они
встретятся?
Решение.
Если Незнайка проходит 3км за полчаса, то его скорость 6км в час, а
Цветика-3км в час. Скорость сближения – 9 км/ч. Значит 3км они пройдут
за 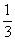 часа, то есть за 20 минут. часа, то есть за 20 минут.
Ответ: 20 мин.
Пока жюри проверяет решения 2 конкурса, команды по очереди
представляют подготовленные сведения из истории математики, а затем
показ презентации.
3 тур. Лингвистический.
1. (3 балла). Напиши вместо пропуска число (буквами, а не цифрами), чтобы получилось истинное предложение:
В ЭТОМ ПРЕДЛОЖЕНИИ _________________________________ БУКВ
(По-русски фраза звучит не совсем правильно).
Ответ: Тридцать четыре.
2. Из слова математика составьте другие слова
(только имена существительные в именительном падеже, нарицательные),
используя при этом для каждого варианта только те буквы, которые есть в
этом слове, например, буква А встречается 3 раза, М – 1раз и т. д. За
каждое придуманное слово-1балл.
4 тур. Геометрический.
1. (3 балла) Из четырех стрелок собрать кленовый лист.
2. (5 баллов)
Разрежьте каждую из этих фигур: прямоугольник 8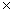 12 и квадрат 2 12 и квадрат 2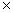 2 на две равные части так, чтобы из них можно было бы сложить квадрат 10×10. 2 на две равные части так, чтобы из них можно было бы сложить квадрат 10×10.
Во время проверки решений, для участников - показ презентации.
5тур. Финальный.
Проводится в том случае, если нельзя выявить или победителя или призера. Предлагается всего одна задача.
1. (5 баллов) Найди наибольшее число, у которого каждая цифра, начиная с третьей, равна сумме двух предыдущих.
Решение.
Пусть x, y – первая и вторая соответственно цифры данного числа, тогда x - любая цифра, кроме нуля.
Тогда
х +y – 3-я цифра,
x + 2y – 4-я цифра,
2x + 3y –5-я цифра,
3x + 5y – 6-я цифра,
5x + 8y – 7-я цифра,
8 x + 13y – 8-я цифра.
Далее процесс заканчивается, т. к. 5x + 8x =13 x > 9, и x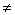 0. Если методом перебора проверять значения x и y, то наибольшим будет число при x =1 и y = 0 (наибольшее число разрядов). 0. Если методом перебора проверять значения x и y, то наибольшим будет число при x =1 и y = 0 (наибольшее число разрядов).
Ответ: 10112358.
Далее жюри подсчитывает количество баллов у каждой команды, называет
команды, которые заняли первое, второе и третье места. Этим командам
вручаются грамоты. Каждый участник викторины, независимо от командного
места, получает «Сертификат участника лицейской викторины». Команде победителей можно вручить символический «Золотой ключ»
|  З В О Н О К НА У Р О К
З В О Н О К НА У Р О К З В О Н О К НА У Р О К
З В О Н О К НА У Р О К