Цели мероприятия:

Введение.

В старинных русских сказках добрый молодец часто стоит перед выбором: "Налево…, вперед…, или направо…?”. И каждое направление сулит какие-то лишения. Современный человек постоянно сталкивается с такой же проблемой выбора пути, вариантов, рисков. Вспомните первый день второй учебной четверти: по давней традиции в этот день мы проводили жеребьёвку к Новому году. Учащиеся случайным образом выбирают бумажку с фамилией ученика класса. Таким образом, вы узнаёте (втайне от остальных), кому должны готовить подарок. И каждый год есть возможность наблюдать яркие картины несовпадения желаемого и полученного результата: "Опять не того достал, кого хотел!”. Вспомните, сколько уже предлагалось решений: "Надо было идти первым!”; "В середине списка – это наверняка!”. Давайте обсудим, можно ли спрогнозировать и достичь желаемого результата? И является ли данный выбор справедливым для всех?

Пути и варианты достижения поставленной задачи складываются в самые разнообразные комбинации. И целый раздел математики, именуемый стохастикой, поможет нам в поисках ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшею.

Соединение элементов теории вероятностей и математической статистики называют стохастикой. Это тот раздел математики, который возник и развивался в тесной связи с практической деятельностью человека. Он позволяет решать задачи, суть которых сводится к определению, является ли право первенства в данной ситуации некоторой привилегией, справедлива ли данная игра, оценить риски, на какую величину сделать ставку, как справедливо выбрать одного из группы, и т.д.

Случайные исходы и события.

Испытания - это любые опыты и исследования, выполнение всевозможных упражнений и операций, а также наблюдения за различными явлениями, процессами которые могут происходить в окружающем нас мире.

Пример. Подбрасывание монеты или кубика – это испытание. Выпадение "орла” или "решки” – исходы подбрасывания монеты.

В жизни под событием понимают любое явление, которое происходит или не происходит. Событиями являются и результаты испытаний (опытов), наблюдений и измерений. Все события можно подразделить на невозможные, достоверные и случайные.

Невозможным называют событие, которое в данных условиях произойти не может. В любом испытании всегда наступает только один исход. В испытании с детерминированным исходом всегда наступает заранее известный исход. В испытании со случайными исходами наступает один из всех возможных исходов.

Пример невозможных событий:

Достоверным (детерминированным) называют событие, которое в данных условиях обязательно произойдёт.

Пример, достоверными являются события:

Случайным называют событие, которое в данных условиях может произойти, а может и не произойти или если результатами испытания могут быть разные исходы, которые нельзя заранее однозначно предсказать, то такие исходы называют случайными.

Пример, случайными являются следующие события:

Человеку всё чаще приходится взвешивать случайные события, классифицировать их исходы как невозможные, возможные и достоверные. Уже давно замечено, что случайностями не так уж редко управляют объективные закономерности. Вот простейший опыт - подбрасывают монету. Выпадение орла или решки, конечно, чисто случайное явление. Но при многократном подбрасывании обычной монеты можно заметить, что появление орла происходит примерно в половине случаев.

Кто и когда впервые проделал опыт с монетой, неизвестно. Французский естествоиспытатель Ж.Л.Л. Бюффон (1707 - 1788) в восемнадцатом столетии 4040 раз подбрасывал монету – орёл выпал 2048 раз. Математик К. Пирсон в начале прошлого столетия подбрасывал её 24000 раз – орёл выпал 12012 раз. Лет 30 назад американские экспериментаторы повторили опыт. При 10000 подбрасываний орёл выпал 4979 раз. Значит, результаты бросаний монеты, хотя каждое из них и является случайным событием, при неоднократном повторении подвластны объективному закону.

Задача 1. Принимая во внимание статистические данные, можно ли считать действия судьи перед футбольным матчем случайными и справедливыми?

Ответ. Да, так как вероятности выпадения орла и решки равны.

Рассмотрим другой, более сложный пример – эксперимент с так называемой доской Гальтона.

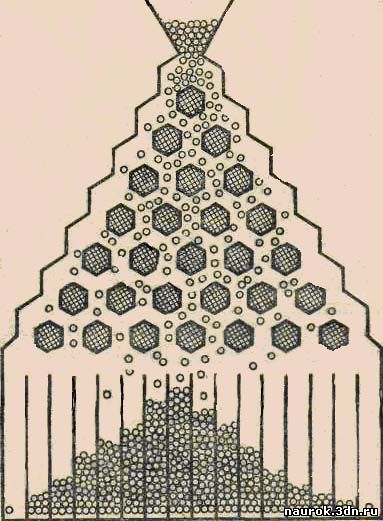
Доска размещена вертикально. Из верхнего резервуара стальные шарики катятся (на отдельных участках падают) вниз и накапливаются в нижних гнёздах. Каждый шарик, встретив на своём пути очередном препятствие, отклоняется или влево или вправо, а затем падает вниз. Шарик, конечно, может попасть в любое из гнёзд. Между тем правильное расположение шариков (симметричное, при котором в центральных гнёздах их много, а в крайних мало), повторяющее от эксперимента к эксперименту, убедительно свидетельствует о существовании объективного закона их распределения.

В 1718 году в Лондоне вышла в свет книга со странным по тем временам названием "Учение о случаях”. Её автор - французский математик А. Муавр (1667- 1754). Муавр измерил рост у 1375 случайно выбранных женщин. Результат - колоколообразная кривая. Самое большое его достижение – открытие закономерности, которая очень часто наблюдается в случайных явлениях. Он впервые заметил и теоретически обосновал роль распределения, которое позднее было названо нормальным.

Наиболее интересные для начинающих задачи теории вероятностей возникли в области азартных игр.

Задача 2. Есть ли среди возможных результатов бросания двух кубиков такой, на который стоит сделать ставку?

(Принимаются гипотезы учащихся).

Решение.

Определим множество всех результатов данного испытания:

W = { 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

Если все возможные результаты испытаний одинаково возможны (одинаково вероятны), то безразлично, на какой из них будет сделана ставка. Если какой-то результат маловероятен, то очевидно, что на него не стоит делать ставку. Ставку следует делать на наиболее вероятный результат. Итак, вопрос о рациональном участии в игре сводится к вычислению (или к оценке) вероятности каждого из возможных результатов испытания.

При бросании двух кубиков ( I, II ) могут получиться следующие равновозможные результаты (всего 36 пар):

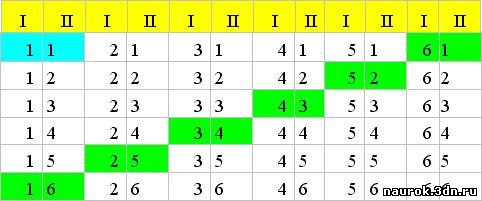
Первая цифра –число очков, выпавших на кубике I, вторая – на кубике II.

С помощью этой матрицы найдём вероятности отдельных результатов бросания двух кубиков. Среди 36 одинаково возможных (одинаково вероятных) случаев только один ведет к сумме 2. Шанс, что, бросая два кубика, мы получим совместно 2 очка, можно оценить как 1/36. А вот сумму в 7 очков можно получить шестью вариантами, значит вероятность этого события – 6/36.

Из статистических данных вытекает, что результаты бросания двух кубиков нельзя считать одинаково вероятными, так как наиболее вероятен исход в 7 очков и менее вероятен в 2 и 12 очков.

Ответ. 7.

Обратите внимание, что ответ в основном не совпал с вашими предположениями.

Вспомним о подбрасывании монеты. Откуда у нас уверенность, что вероятность выпадения орла равна ?? Почему интуиция подвела в случае с кубиками?

Факты, обнаруживающие, что объективная реальность необязательно совпадает с человеческим "кажется”, послужили причиной статистической оценки возможности появления события.

Вернёмся к нашей предновогодней жеребьёвке.

Задача3. Путём случайного выбора учащиеся устанавливают, кто для кого готовит новогодний подарок. У тебя в классе есть "симпатия”, и ты хотел бы, чтобы твои шансы вытащить бумажку с её фамилией, были максимальны. Когда лучше тянуть жребий: первым, позже или это не имеет значение?

Решение. Пусть в классе а мальчиков и b девочек, всего (а + b) = n учащихся. Заменим бумажки с именами мальчиков на черные шары, каждый занумеруем (от 1 до а). Бумажки с именами девочек - занумерованными белыми шарами (от а + 1 до n).

Случайно выбираем n раз шар без возвращения. Возможны следующие события:

С₁={ вынутый в первый раз шар будет белым} ,

С₂={ вынутый во второй раз шар будет белым} ,

…………………………………………………..

С_а+в={ вынутый в n раз шар будет белым} . Найти вероятность этих событий.

Теперь выбираем по очереди шары из урны и размещаем в ряд, один за другим. Таким образом, шар, случайно выбранный в первый раз, попадёт на первое место, шар, вынутый во вторую очередь, попадёт на второе место и т.д. Возникшую таким образом последовательность шаров можно рассматривать как числовую – своеобразный протокол случайного выбора шаров. Она так же является результатом данного случайного испытания. Автором порядка следования шаров является случай. Любой результат случайного испытания является перестановкой (расстановка элементов конечного множества в последовательность 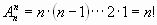) множества номеров шаров. Если определить мощность множества W всех результатов данного испытания, то легко заметить, что всех возможных вариантов n(n-1)(n-2)... 3*2*1=n!

Событию С₁ благоприятствуют те перестановки, первый член которых является номер белого шара. Таких перестановок можно получить b штук. Остальные n-1 шаров можно разместить на (n-1) позиции (n-1)! способами. Учитывая, что n!= n? (n-1)!, имеем

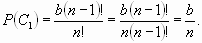
Аналогично рассуждая, получаем .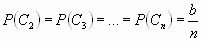

Таким образом, безразлично, каким по счету ты будешь в очереди для выбора бумажки с именем.

Ответ. Не имеет значения.

В жизни мы часто пользуемся фразами (исходя из своего жизненного опыта объясните их смысл):

" Это невероятно!”,

"Маловероятно, что сегодня будет дождь”,

"Сто процентов – это будет”, "Наверняка это случится!”, "Я уверен, что это произойдет!”,

" Пятьдесят на пятьдесят”, "Шансы равны”, " Один к одному”.

Каждый раз, когда вы будете употреблять эти выражения, в связи с каким-нибудь выбором, вспомните, что статистика и вероятность могут обосновать ваши предположения или развеять их, а значит, помогут принять верное решение.