Форма мероприятия: игра.
- развитие познавательного интереса к
геометрии, математике, интеллекта учащихся,
- расширение кругозора, знаний и воспитание
дисциплинированности, стремления к их
непрерывному совершенствованию,
- формирование чувства солидарности и здорового
соперничества,
- привитие учащимся интереса к предмету с помощью
изучения истории и развития науки.
Оборудование:
- крутящийся барабан со стрелкой;
- две шкатулки;
- ящик;
- призы;
- мультимедийный проектор.
Программа игры.
- Музыкальное вступление.
- Математическое вступление.
- Ознакомление с условиями игры.
- Отбор первой тройки игроков.
- Игра первой тройки.
- Отбор второй тройки игроков.
- Игра второй тройки.
- Отбор третьей тройки игроков.
- Игра третьей тройки.
- Игра со зрителями.
- Финал.
- Супер игра.
- Заключительное слово.
У ведущего два помощника, которые фиксируют
ответы, следят за порядком игры.
ХОД ИГРЫ
I. Музыкальное вступление.
Звучат позывные программы капитал-шоу "Поле
чудес”.
II. Математическое вступление.
Музыкальное выступление учащихся 5
класса. Исполняют песню на мотив "Учат в
школе”(слова М. Пляцковского, музыка В.
Шаинского)
Cтихотворение "Гимн математике”
Чтоб водить корабли,
Чтобы в небо взлететь,
Надо многое нам узнавать,
И при этом, и при этом,
Вы заметьте-ка, заметьте
Очень важная наука
Мате-ма-тика!
Почему корабли
Не садятся на мели,
А по курсу идут
Сквозь туман и метель?
Потому что, потому что,
Вы заметьте-ка, заметьте
Капитанам помогает
Мате-ма-тика!
Чтоб врачом и моряком
Или лётчиком нам стать.
Надо прежде всего
Математику знать.
И на свете нет профессий
Вы заметьте-ка, заметьте
Где бы вам не пригодилась
Мате-ма-тика!
Ведущий: Уважаемые участники игры. Сегодня мы
с вами посвятим нашу игру самой древней науке –
геометрии. В переводе с греческого слово
"геометрия” означает "землемерие” ( от ge
"гео” - по-гречески земля и metrein "метрео”—
мерить) . Такое название объясняется тем, что
зарождение геометрии было связано с различными
измерительными работами, которые приходилось
выполнять при разметке земельных участков,
проведении дорог, строительстве зданий и других
сооружений. Ее возникновение уходит в глубь
тысячелетий и связано прежде всего с развитием
ремесел, культуры, искусств, с трудовой
деятельностью человека и наблюдением
окружающего мира.
Древние египтяне были замечательными
инженерами. До сих пор не могут до конца
разгадать загадки огромных гробниц Египетских
царей – Фараонов.
Геометрия является важной учебной дисциплиной
для многих профилей обучения. Она необходима
будущим строителям и архитекторам, химикам и
инженерам, агрономам. Геометрия не только дает
представление о фигурах, их свойствах, взаимном
расположении, но и учит рассуждать, ставить
вопросы, анализировать, делать выводы, то есть
логически мыслить. Я хочу, чтоб вы сегодня
убедились, что геометрия – такая же интересная
наука и что заниматься ею так же увлекательно.
Надеюсь, что сегодня на игре нам будет интересно
и весело.
III. Условия игры.
Ведущий: Теперь познакомлю вас с условиями
игры.
Игра проходит по аналогии программы капитал –
шоу "Поле чудес”. В ходе игры каждый участник
имеет возможность передать привет другу,
учителю, зрителям. Форма привета – песня,
стихотворение, собственная поделка и т.д.
Если участник игры отгадает три буквы, то он
имеет возможность выбрать одну из двух
предложенных шкатулок: одна пустая, в другой
приз.
Если выпадает приз, то ассистент выносит ящик, в
котором находится приз (тетрадь, ручка, линейка и
т.д.).
Если ученику выпадает сюрприз, то он вытягивает
билет с заданием; если отвечает, то остается в
игре, называет букву; если не отвечает правильно,
то остается в игре с передачей хода .
Если выпадает шанс, то можно выбрать из зала
помощника, и он называет букву, а ученик может
использовать подсказку, но может принять свое
решение.
На барабане с вращающимся волчком: числа -
количество очков; "С"-сюрприз; " + " очки
удваиваются, если он верно назовёт букву (если
две буквы, то утраивается, если три — умножается
на 4, и т. д.); "Б" – банкрот, П – приз, Ш – шанс,
Ноль (0) — набранные очки не сгорают, но ход
передаётся другому игроку..
После того, как слово разгадано, участники
занимают места в зале.
IV. Отбор первой тройки игроков.
Вопросы отбора первой тройки игроков.
- Каким свойством обладают вертикальные углы?
- Чему равна сумма смежных углов?
- Какие приборы применяют для построения прямых
углов на местности? (Экер, теодолит)
V. Игра первой тройки.
Под музыку выходит первая тройка игроков и
занимает места у барабана и ведущий представляет
их, сообщает имя, класс.
Задание. Он крупнейший мыслитель древней
Греции - считается одним из первых
древнегреческих геометров и философов. Был
крупнейшим астрономом. Он первый в истории науки
предсказал солнечное затмение 23 мая 585 года до
новой эры. Ему принадлежит открытие следующих
теорем:
- Вертикальные углы, полученные при пересечении
двух прямых линий, равны.
- В равнобедренном треугольнике углы, лежащие при
основании, равны.
- Круг делится диаметром пополам.
- Угол, вписанный в полуокружность, прямой и
другие.
Вопрос. Кто он?
| Ф |
А |
Л |
Е |
С |
|
М |
И |
Л |
Е |
Т |
С |
К |
И |
Й |
| 1 |
2 |
3 |
4 |
5 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
Выступление 7 класса.
Греческие авторы относят появление геометрии в
Греции к концу VII в. до н. э. и связывают его с
именем Фалеса Милетского (639—548). Купец в
свободное время занимался математикой. И сделал
величайшее открытие: обнаружил, что многие
геометрические закономерности можно получать не
опытным путем, а с помощью рассуждения
(доказательства). Это формулируют так: накрест
лежащие углы, получающиеся при пересечении двух
параллельных прямых третьей прямой, равны. Фалес
доказал и ряд других теорем.
Oснователь милетской школы, один из легендарных
"семи мудрецов".
Происходил из аристократического рода, был
связан с храмом Аполлона Дидимского, патрона
морской колонизации. Имя Фалеса уже в V в. стало
нарицательным для мудреца. Считается, что Фалес
ввел в употребление новое созвездие - Малую
Медведицу.
Фалеса называют одним из первых греческих
мыслителей, кто понял важность астрологии как
науки. В историю вошло "затмение Фалеса" 28
мая 585 г. до н.э., предсказанное им за 6 лет до
события (некоторые ученые считают это легендой,
доказывая, что уровень развития науки во времена
Фалеса еще не позволял предсказывать затмения). В
честь Фалеса названа малая планета 6001 Thales
VI. Вопросы отбора второй тройки игроков.
- Сформулируйте теорему о сумме углов
треугольника.
- Какой треугольник называется тупоугольным?
- Что называется расстоянием от точки до прямой?
(Длина перпендикуляра, проведенного из точки к
прямой)
VII. Игра второй тройки.
Звучит музыка. Ведущий приглашает вторую
тройку игроков к барабану и представляет их.
Задание. Девизом каждого, кто нашел что-то
новое, является слово "Эврика!” Именно так
воскликнул этот ученый, открыв новый закон. Он же
с большой точностью вычислил значение 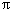 – отношение длины окружности к ее
диаметру. Он изобрел машину для орошения полей.
Впервые для поднятия тяжестей стал применять
систему рычагов и блоков. Кто он? – отношение длины окружности к ее
диаметру. Он изобрел машину для орошения полей.
Впервые для поднятия тяжестей стал применять
систему рычагов и блоков. Кто он?
| А |
Р |
Х |
И |
М |
Е |
Д |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
Выступление 8 класса.
Заслуга Архимеда заключалась в том, что он
установил теоретические основы, на которых в
конечном счете и по сей день покоится
машиностроение, — он фактически создал основы
механики. Механика требовала вычисления масс, а
следовательно, площадей и объемов, а также
Центров тяжести; механика настоятельно
требовала метрической геометрии; на этом и
сосредоточено внимание Архимеда в геометрии. До
нас дошли следующие сочинения Архимеда: две
книги "О шаре и цилиндре”, "Об измерении
круга”, две книги "О равновесии плоскости”, "О
квадратуре параболы”, "О плавающих телах” и.т.д.
VIII. Вопросы отбора третьей тройки.
- Каким инструментом измеряют углы на местности?
(Астролябия)
- Какие два отрезка называются параллельными?
(Если они не пересекаются)
- Какой инструмент используется для разметки
параллельных прямых при выполнении столярных
работ? (Малка)
IX. Игра третьей тройки
Звучит музыка. Ведущий приглашает третью
тройку игроков к барабану и представляет их.
Задание. Этот ученый участвовал в
атлетических состязаниях и на олимпийских играх
был дважды увенчан лавровым венком за победу в
кулачном бою. Ему принадлежит открытие следующих
теорем:
1. Теорема о сумме внутренних углов
треугольника.
2. Деление плоскости на правильные
многоугольники.
3. Геометрические способы решения квадратных
уравнений
4. Деление чисел на чётные и нечетные, простые и
составные
5. Доказательство того, что v2 не является
рациональным числом и другие.
Кто он?
| П |
И |
Ф |
А |
Г |
О |
Р |
|
С |
А |
М |
О |
С |
С |
К |
И |
Й |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Выступление 9 класса.
Пифагор родился в 580 г. до н.э. на острове Самос, в
семье богатого ювелира. Его учителями были
Гермодамант, Ферекид, Фалес.
Знания, полученные им в храмах Греции не давали
ответов на все волнующие его вопросы, и он
отправился в поисках мудрости в Египет.
Когда Пифагор постиг науку египетских жрецов,
то засобирался домой, чтобы там создать свою
школу. Жрецы, не желавшие распространения своих
знаний за пределы храмов, не хотели его
отпускать. С большим трудом ему удалось
преодолеть эту преграду.
Однако по дороге домой Пифагор попал в плен и
оказался в Вавилоне. Вавилоняне ценили умных
людей, поэтому он нашел своё место среди
вавилонских мудрецов. Пифагор прожил в Вавилоне
около десяти лет и в сорокалетнем возрасте
вернулся на родину. Но на острове Самос он
оставался недолго, а поселился в одной из
греческих колоний Южной Италии в городе Кротоне.
Пифагор сделал много важных открытий, но
наибольшую славу ученому принесла доказанная им
теорема, которая сейчас носит его имя .
Известно открытие Пифагора в области теории
музыки. Для воплощения своего открытия Пифагор
использовал монохорд – полуинструмент,
полуприбор. Под струной на верхней крышке ученый
начертил шкалу, с помощью которой можно было
делить струну на части. Было проделано много
опытов, в результате которых Пифагор описал
математически звучание натянутой струны.
X. Игра со зрителями
Кто из русских писателей является автором
учебника для детей под названием "Арифметика”?
| Т |
О |
Л |
С |
Т |
О |
Й |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
Ведущий:
Великий русский писатель Лев Николаевич
Толстой проявлял особый интерес к математике и
ее преподаванию, много лет преподавал начало
математики в основанной им же Яснополянской
школе и написал оригинальный учебник
"Арифметика”.
XI. Финал
Ведущий приглашает финалистов к барабану и
представляет их.
Задание.
Вся творческая жизнь нашего выдающегося
соотечественника была связана с Казанским
университетом, где он учился, затем был
профессором, а с 1827г.-ректором университета. Он
предпринял попытку доказать пятый постулат от
противного. Он не получил противоречивых
утверждений. На основании этого им был сделан
вывод: можно построить другую геометрию,
отличную от геометрии Евклида. Сообщение о
построении геометрии им было сделано в 1826г. Эта
геометрия теперь называется неевклидовой. Это
гениальное открытие принадлежит кому?
| Л |
О |
Б |
А |
Ч |
Е |
В |
С |
К |
И |
Й |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
Выступление 9 класса.
Коренной перелом в геометрии впервые произвел
в первой половине ХIХ в. великий русский
математик Николай Иванович Лобачевский, который
создал новую, неевклидову геометрию,
называемую ныне геометрией Лобачевского.
Открытие Лобачевского было началом нового
периода в развитии геометрии. Неевклидова
геометрия сыграла огромную роль во всей
современной математике. Предположение
Лобачевского, что реальные геометрические
отношения зависят от физической структуры
материи, нашло подтверждение не только в
космических масштабах. Современная теория квант
все с большей настоятельностью выдвигает
необходимость, применения геометрии, отличной от
евклидовой, к проблемам микромира.
В е д у щ и й
Жюри подсчитывает заработанные победителем
игры очки и объявляет их. Вносится плакат:
"Список призов за заработанные очки”.
| Призы |
Очки |
| Набор линеек |
100 |
| Набор ручек |
200 |
| Общая тетрадь |
150 |
| 4. Фотоальбом |
400 |
| 5. Сладкий приз |
250 |
| 6. Набор карандашей 150 |
|
| Шкатулка с сюрпризом |
300 |
| 8. Блокнот |
150 |
| 9. Транспортир |
50 |
| 10. Фломастеры |
80 |
Победитель выбирает на набранное количество
очков призы.
Ведущий предлагает суперигру победителю.
Предложение принимается.
XII. Суперигра
Задание.
Название фигуры "трапеция” происходит от
греческого слова "трапезион”. Как оно
переводится на русский язык?
Разрешается открыть любые две буквы. Дается 1
минута на размышление.
XIII. Заключение
Итак, мы закончили игру. Поздравляем (Ф.И.
победителя) с победой и желаем дальнейших
успехов.
Геометрические знания широко применяются в
жизни — в быту, на производстве, в науке. И если
ты, хорошо изучил курс геометрии, то не
останешься безоружным, когда при решении
практических задач потребуется применить
геометрические теоремы или формулы. В настоящее
время геометрия тесно переплетается со многими
другими разделами математики.
Надеемся, вы сегодня узнали много интересного
из курса раздела геометрии.
|  З В О Н О К НА У Р О К
З В О Н О К НА У Р О К З В О Н О К НА У Р О К
З В О Н О К НА У Р О К