Конкурс «Головоломка»

Всем читателям газеты, любителям занимательной математики предлагаем принять участие в конкурсе по решению математических головоломок. Надеемся, что вместе со взрослыми активное участие в конкурсе примут юные, пытливые умы – учащиеся школ района. Уровень сложности задач позволит им это сделать.
Конкурс пройдет в 5 туров, по три задачи в каждом. Вместе с ответами на задачи участники должны сообщить фамилию, имя, отчество, домашний адрес, возраст ирод занятий.
При определении победителей по итогам всех туров будут учитываться: количество правильно решенных задач, полнота решения задачи.
Победители конкурса награждаются дипломами и памятными подарками. За первое место будет вручена головоломка «Причеши ежа» – модификация известного всему миру кубика Э. Рубика.

Задания первого тура

1.  Заполните пустые клетки  квадрата буквами 3, А, Р, Я так, чтобы в каждом горизонтальном и в каждом вертикальном рядах и в диагоналях квадрата каждая буква встречалась один раз.

2. Постройте замкнутый обход шахматным конем всех клеток доски, изображенной на рисунке, не заходя в одну и ту же клетку дважды.

3.  В кружки фигуры впишите числа от 1 до 9 так, чтобы сумма четырех чисел, расположенных в кружках-вершинах всех квадратов (их 6), была равна 20.

Итоги первого тура

Закончился первый тур конкурса любителей занимательной математики – «ГОЛОВОЛОМКА». Предложив желающим принять участие в этом состязании, жюри конкурса даже не предполагало, что столько наших читателей разных возрастов: и школьников, и вполне солидных людей – заинтересуются решением, на первый взгляд простых, но очень интересных задач.

Задача 1 имеет два решения, в левом нижнем углу квадрата можно написать либо букву А, либо Р, а, следовательно, возможны два варианта решений.

Самой трудной задачей первого тура оказалась задача  2. Полностью с ней справились только пять участников.
Весьма оригинальное, но простое и красивое решение этой задачи прислал Федоров. Он заметил, что фигуру можно разделить на четыре равные части. Сделав конём замкнутый обход на одной части, он объединил их в единый замкнутый обход коня по всем клеткам многоугольника.

Задача 3 имеет единственное решение.

Задания второго тура

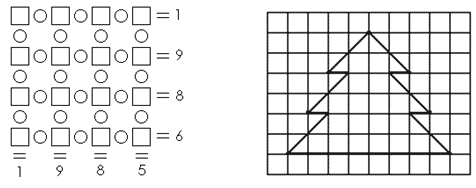
4. В квадраты расставьте числа от 1 до 16, а в кружки знаки +, –, ·, : так, чтобы получилось восемь верных равенств.

5. На рисунке изображена елочка. Разрежьте ее на пять частей так, чтобы из них можно было сложить квадрат.

6. В зашифрованном тексте «ШЪУЯЪТ ЛНПЪИРЭ Э СРЭРТ ЬРЫЛ» каждая буква заменена буквой русского алфавита по закону, связанному с одним из понятий геометрии. Установите этот закон и расшифруйте текст. Например, слово ТАЗ расшифровывается как слово МЯЧ.

Итоги  второго тура

Для тех, кто не справился с этой задачей, приводим решение.

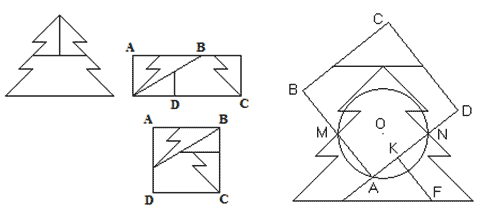
Трудной оказалась задача 5. Полностью с ней справились лишь два участника. На рисунке показано авторское поэтапное прeвращение елочки в квадрат. Сначала у нее срезается «верхушка» и она превращается в прямоугольник, затем отмечаются отрезки АВ и СD, равные стороне будущего квадрата, и производится еще два разреза. В результате получаем пять частей, из которых складывается квадрат АВСD.

Преподаватель математики из Новошахтинска А.М. Домашенко пишет: «Задача о елочке буквально не давала мне покоя (за что выражаю свою признательность её автору)». После «долгих размышлений» ему удалось улучшить авторское решение задачи, найдя более экономное разрезание – всего на четыре части. Этим он приятно удивил членов жюри.
Вот как А.М. Домашенко удалось разрезать елочку на 4 части: «Из центра елочки (точка О) проводится окружность радиусом 2 см. Из точки М проводится окружность радиусом 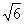. Точка А пересечения этих окружностей является первой вершиной квадрата. Соединив ее с точками М и  N и продолжив прямые дальше, отметим точки В и D так, что ВМ = АМ и АD = АВ. Из точки N проводим окружность радиусом ND и отмечаем на отрезке АD точку К. Восстанавливаем перпендикуляр KF и достраиваем квадрат АВСD. Осталось разрезать елочку и сложить квадрат». Поздравляем Александра Михайловича с таким виртуозным разрезанием елочки.

Задача 6 решена всеми участниками второго тура. Здесь была зашифрована фраза: «Желаем успеха в Новом году». 

Задания третьего тура

7. Четырёхзначное число ЗАРЯ – точный квадрат. Кроме этого для его цифр выполняется равенство: З x А x Р x Я = ЗА + РЯ. Найдите число ЗАРЯ, зная, что одинаковыми буквами здесь обозначены одинаковые цифры, разными – разные.

8. Спичками напишите слово «ЗАРЯ» так, как это сделано на рисунки. Теперь на это слово наложите нитку подходящей длины так, чтобы нитка проходила через каждую спичку, причём только по одному разу. Укажите один из вариантов.

9. В парке на скамейке беседовали группа ребят: Андрей, Борис, Витя, Гена и Дима – учащиеся 6, 7, 8, 9 и 10 классов. Из их разговора удалось установить, что:

1) Андрей дружит с шестиклассником;
2) девятиклассник вместе с Андреем и Борей посещают математический кружок;
3) Гене и Диме предстоит в этом году сдавать экзамен;
4) Витя учится в более старшем классе, чем Гена.
Установите, в каком классе учится каждый из этих мальчиков?

Итоги третьего тура

Подведены итоги третьего этапа математического конкурса. Задача 7 оказалась «крепким орешком», и поиск квадратного числа у многих участников конкурса вызвал затруднения. Условию задачи удовлетворяют два числа – 1296 и 9216. Автор этой задачи В. Тимченко пишет: «Не скрою, приятно видеть свою задачу в числе конкурсных, но все же задача №5 «Квадрирование ёлочки» понравилась больше».

С задачей 8 справились практически все участники. На рисунке показан один из способов решения. Хитрость задачи состоит в том, что накладывать нитку нужно начинать с внутренней части буквы «А», заканчивать во внутренней части буквы «Я».

Как следует из почты, задача  9 оказалась наиболее легкой. Она имеет такой ответ:  Боря – в шестом классе, Андрей – вседьмом, Гена – в восьмом, Витя – в девятом,   Дима – в   десятом   классе.

Задания четвертого тура

10. Сколько треугольников вы сможете насчитать в фигуре, изображенной на рисунке?

11. Десятикопеечную монету нужно разменять медными монетами (1, 2, 3 и 5 копеек). Сколькими способами это можно сделать?

12. Из полного набора домино (28 косточек), прикладывая косточки друг к другу одинаковыми значениями очков, выложите фигуру, изображенную на рисунке. Достаточно указать одно решение.

Членам жюри не удалось решить эту задачу, но и не удалось доказать, что решения не существуют. За решение этой задачи учрежден специальный приз – книга по занимательной математике «В царстве смекалки». Ею будет награжден читатель, первым приславший решение этой задачи в редакцию газеты.

Итоги четвертого тура

В фигуре, приведенной к задаче 10, можно насчитать 60 различных треугольников.
В задаче 11 монету достоинством 10 копеек можно разменять медными монетами 20-ю способами.

Задача №12, как и ожидалось, оказалась наиболее трудной. Большинство участников пытались указать конкретное расположение косточек домино. А.М. Домашенко и В.Н. Тимченко с помощью логических рассуждений доказали, что расположить косточки согласно условию задачи невозможно.

Задания пятого тура

13. Из полного комплекта домино (28 косточек) сложен прямоугольник 7 х 8, но на рисунке не обозначены границы костей. Восстановите положение костей. Достаточно указать одно расположение.

14. Впишите в кружки числа так, чтобы каждое следующее в направлении стрелки число получилось из предыдущего при помощи действия, указанного рядом со стрелкой.

15. На рисунке приведен пример на умножение. В нем некоторые цифры заменены буквами, а остальные точками, причем, одинаковым буквам соответствуют одинаковые цифры, разным – разные. Определите число ЗАРЯ.

Внимание! Жюри просит всех участников конкурса, в ответах на задание 5 тура указать одну, наиболее интересную на ваш взгляд из 15 задач нашего конкурса «Головоломка». Таким способом будет выбрана лучшая головоломка конкурса. Автор этой задачи будет награжден специальным призом.

Итоги пятого тура

Как отмечает в своем письме мама и сын Ютины: «Задача 13 оказалась наиболее интересной и неожиданно трудной, возникает много вариантов, отчего перебор становится очень трудным. Но нам удалось».

На рисунке приведен комплект домино с восстановленными границами. Это один из возможных вариантов.

Всего существует 10 вариантов. Это показали в своих ответах В. Тимченко, А. Воронков и А. Домашенко. Они смогли организовать системный перебор вариантов и не упустили ни одного. Вот что значит математическая подготовка. Их ответы оценены в 1,1 балла.

Заметим для справки: впервые головоломки на восстановление границ домино предложил польский кинокритик Л. Пияновский.

Методом проб и ошибок трудно найти решение задачи 14. Но если одно из чисел этой числовой карусели обозначить буквой х, то, выражая через х числа других кружков в направлении стрелок,  нетрудно составить и решить уравнение. Это уравнение может быть таким, ((х + 1) · 2 · 3 : 4 · 5 : 6 · 7 – 8) : 9 = х, если через х обозначить число самого верхнего кружка. Корнем этого уравнения является число 3, поэтому числовая карусель примет вид 3, 4, 8, 24, 6, 30, 5, 35, 27. Расстановка чисел – единственна.
Должен отметить, что эта задача близка к школьному курсу алгебры, поэтому не случайно среди правильно решивших её много учащихся.

Задача 15  по сути –  арифметическая, для её решения достаточно знать только правило умножения многозначных чисел. Имеет единственное решение ЗАРЯ = 9376, и оказалась для многих участников совсем не простой.