Цели урока:
- сформировать понятие вписанного угла, изучить
теорему о вписанном угле;
- формирование навыков самостоятельной работы с
учебником.
Структура урока:
- Постановка цели урока.
- Актуализация знаний и умений.
- Формирование понятия вписанного угла.
- Изучение теоремы о вписанном угле.
- Применение теоремы.
- Подведение итогов работы на уроке.
- Задание на дом.
Ход урока
I. Организационный момент.
II. Актуализация знаний и умений.
Задание на готовом чертеже:
Найдите угол АВС, если 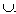 АС = 70° . АС = 70° . Нельзя ли указать угол, связанный с 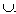 АС, зная который
можно найти АС, зная который
можно найти  АВС? АВС?
Таким углом является  АОС. АОС.
 АОС = 70°
(материал предыдущего урока). АОС = 70°
(материал предыдущего урока).
Так как треугольник АВО равнобедренный (АО
= ВО радиусы окружности), то  ВАО = ВАО =  АВО. Следовательно, АВО. Следовательно,  АОС = 2 АОС = 2 АВО, откуда АВО, откуда  АВО = 35° . АВО = 35° .
Угол, вершина которого лежит на окружности, а
стороны пересекают окружность, называется вписанным
углом.
 АВС
вписанный: АВС
вписанный:
1) вершина В лежит на окружности;
2) сторона ВА пересекает окружность;
3) сторона ВС пересекает окружность.
III. Формирование новых знаний и умений.
Какие из углов, изображенных на рисунке 1,
являются вписанными? Укажите изображенные на рисунке 2 вписанные
углы (слайд презентации). Вписанные углы 4 и 5 образуют угол, также
являющийся вписанным.
Выполненное в начале урока задание привело нас
к выводу: вписанный угол измеряется половиной
дуги, на которую он опирается. Теперь это
утверждение нам нужно доказать.
Учитель на доске, а учащиеся в тетрадях
выполняют рисунок, делают записи.
Теорема:
Вписанный угол измеряется половиной дуги, на
которую он опирается.
На доске:
Дано:
Окр.(O, R)
угол ABC - вписанный угол,
опирающийся на дугу АС.
Доказать:
 АВС = 1/2 АВС = 1/2 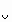 АС. АС.
Доказательство:
(Оформление доказательства учащиеся выполняют
самостоятельно).
Рассмотрим случай, когда луч ВО совпадает с
одной из сторон угла АВС.
Например, со стороной ВС. В этом случае дуга АС
меньше полуокружности, поэтому  АОС равен дуге АС. Так
как АОС равен дуге АС. Так
как  АОС –
внешний угол равнобедренного треугольник АВО,
а углы 1 и 2 при основании равнобедренного
треугольника равны, то АОС –
внешний угол равнобедренного треугольник АВО,
а углы 1 и 2 при основании равнобедренного
треугольника равны, то  АОС = АОС =  1 + 1 +  2 = 2
* 2 = 2
*  1. Отсюда
следует, что 2 * 1. Отсюда
следует, что 2 *  1
= 1
= 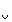 АС или АС или  АВС = АВС =  1 = 1/2 1 = 1/2 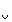 АС. АС.
Вопрос к учащимся:
А какие еще могут быть рассмотрены случаи
расположения луча ВО относительно угла АВС?
(Доказательство теоремы во втором и третьем
случаях учащиеся рассматривают самостоятельно,
при этом учитель показывает, как эти случаи
сводятся к первому случаю.)
Следствие 1: Вписанные углы, опирающиеся на
одну и ту же дугу, равны.
Следствие 2: Вписанный угол, опирающийся на
полуокружность - прямой.
IV. Закрепление нового материала.
1. Решить устно: № 653
Найдите вписанный угол АВС, если дуга АС,
на которую он опирается, равна: а) 48° ; б) 57° ; в) 90° ;
г) 124° ; д) 180° ;
№ 654
По данным рисунка найдите х.
2. Решить письменно: № 655, № 656, № 658.
№ 655
Центральный угол АОВ на 30° больше
вписанного угла, опирающегося на дугу АВ. Найдите
каждый из этих углов.
№ 656
Хорда АВ стягивает дугу, равную 115° , а хорда АС
– дугу в 43° . Найдите угол ВАС.
№ 658
Через точку А к данной окружности проведены
касательная АВ (В - точка касания) и
секущая АD, проходящая через центр О (D
– точка на окружности, О – лежит между А и
D). Найдите  ВАD
и ВАD
и  АDВ, если АDВ, если 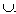 ВD = 110° 20' . ВD = 110° 20' .
V. Итоги урока.
Вопросы к учащимся:
- Какой угол называется центральным?
- Чему равна градусная мера центрального угла?
- Какой угол называется вписанным?
- Чему равна градусная мера вписанного угла?
- Что можно сказать о градусной мере вписанных
углов, опирающихся на одну и ту же дугу?
- Чему равна градусная мера вписанного угла,
опирающегося на полуокружность?
VI. Домашнее задание:
п. 71; вопросы 11-13 (стр.187), № 657, № 660.
11. Какой угол называется вписанным?
Сформулируйте и докажите теорему о вписанном
угле.
12. Докажите, что вписанные углы, опирающиеся на
одну и ту же дугу, равны.
13. Докажите, что вписанный угол, опирающийся на
полуокружность, прямой.
№ 657
Точки А и В разделяют окружность на две
дуги, меньшая из которых равна 140° , а большая
точкой М делится в отношении 6 : 5, считая от
точки А. Найдите угол ВАМ.
№ 660
Через точку, лежащую вне окружности, проведены
две секущие, образующие угол в 32° . Большая дуга
окружности, заключенная между сторонами этого
угла, равна 100° . Найдите меньшую дугу.
|  З В О Н О К НА У Р О К
З В О Н О К НА У Р О К З В О Н О К НА У Р О К
З В О Н О К НА У Р О К