Цели урока:
1. Познакомиться с новыми областями науки. Продемонстрировать связь таких наук как геометрия, алгебра и информатика.
2. Познакомиться с принципами построения геометрических фракталов.
3. Рассмотреть подобие различных геометрических фигур на примере геометрических фракталов.
4. Повторить формулу n-ого члена геометрической прогрессии.
Ход урока
1. Рассмотреть галерею фракталов.
2. Заслушать сообщение учащихся об истории возникновения фрактальной геометрии.
3. Дать определение фракталов.
Определение фрактала, данное Мандельбротом, звучит так: «Фракталом
называется структура, состоящая из частей, которые в каком-то смысле
подобны целому».
4. Размерность фракталов.
Одной из идей, выросших из открытия фрактальной геометрии, была идея
нецелых значений для количества изменений в пространстве. Мы знаем,
что Евклидова геометрия изучает фигуры с размерностью 1, 2, 3 (длина,
ширина, высота). Фигуры с размерностью 1- это отрезок, с размерностью
2- фигура на плоскости (например, квадрат, трапеция, треугольник), 3-
геометрические тела (например, куб, шар, пирамида и т.д.)
Одним из основных свойств фракталов является самоподобие. В самом
простом случае небольшая часть фрактала содержит информацию о самом
фрактале.
Если смотреть с математической точки зрения, то размерность определяется следующим образом.
Для одномерных объектов - увеличение в 2 раза линейных размеров
приводит к увеличению размеров (в данном случае длины) в 2 раза, т.е. в
21.
Для двухмерных объектов увеличение в 2 раза линейных размеров приводит к увеличению размера (площади) в 4 раза, т.е. в 22. Приведем пример. Дан круг радиуса r, тогда S= π r2.
Если увеличить в 2 раза радиус, то: S1 = π(2r2 ); S1= 4πr2 .
Для трехмерных объектов увеличение в 2 раза линейных размеров приводит к увеличению объема в 8 раз, т.е. 23.
Если мы возьмем куб, то V=а3, V'=(2а)3=8а; V'/V= 8.
Однако природа не всегда подчиняется этим законам. Попробуем рассмотреть размерность фрактальных объектов на простом примере.
Представим себе, что муха хочет сесть на клубок шерсти. Когда она
смотрит на него издалека, то видит только точку, размерность которой 0.
Подлетая ближе, она видит сначала круг, его размерность 2, а затем шар
– размерность 3. Когда муха сядет на клубок, она шара уже не увидит, а
рассмотрит ворсинки, нитки, пустоты, т.е. объект с дробной
размерностью.

Размерность объекта (показатель степени) показывает, по какому
закону растет его внутренняя область. Аналогичным образом с ростом
размера возрастает «объем фрактала». Ученые пришли к выводу, что фрактал - это множество с дробной размерностью.
5. Рассмотреть принцип построения геометрических фракталов.
Фракталы этого класса самые наглядные. В них сразу видна самоподобность.
Их получают путем простых геометрических построений. Поступают
следующим образом: берется отрезок или геометрическая фигура, на
основании которых будет строиться фрактал. Далее выбирается набор
правил, который преобразует наш отрезок в новую геометрическую фигуру.
Затем к каждой части получившейся фигуры применяют тот же набор правил.
С каждым шагом фигура будет становиться все сложнее и сложнее. И если
мы проведем большое количество преобразований, то получим
геометрический фрактал.
5.1 Задание №1
Построить геометрический фрактал «Кривая Коха» Рассмотреть самоподобность отдельных элементов фрактала.
Рассчитать длину отрезка после 5 генераций. Рассчитать длину отрезка
после 5 генераций, если длина первоначального отрезка 10 см.
5.2 Задание №2
Рассмотрим «Треугольник Серпинского». Для этого берём равносторонний
треугольник, затем отмечаем середины сторон. проводим средние линии и
исключаем средний треугольник. В оставшихся трёх треугольниках опять
проводим средние линии и исключаем средние треугольники и т.д. Если мы
теперь возьмем любой из образовавшихся треугольников и увеличим его –
получим точную копию целого. В данном случае имеем дело с полным
самоподобием. «Смоделировать геометрический фрактал «Треугольник Серпинского» и рассчитать площадь треугольника после 10 генераций».
Решение:
Пусть сторона треугольника равна 32 см.
Найдем площадь 10-ого треугольника S10=?
Мы знаем формулу для нахождения n-ного члена геометрической прогрессии: b10 = b1*q^(n-1)
q=1/2, значит b10=32*(1/2)^9, b10=1/16.
S10=1/2* b210*sin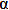 , , 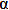 =60o, т.к. треугольник равносторонний. =60o, т.к. треугольник равносторонний.
S10=1/2*b210*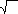 3/2, 3/2,
S10=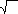 3/1024 мс. 3/1024 мс.
Ответ:  3/1024 см. 3/1024 см.
6. Показать применение геометрических фракталов в науке и технике на примере телекоммуникаций.
Использование фрактальной геометрии при проектировании антенных
устройств было впервые применено американским инженером Натаном Коэном,
который жил тогда в центре Бостона, где была запрещена установка на
зданиях внешних антенн. Коэн вырезал из алюминиевой фольги фигуру в
форме кривой Коха и затем наклеил ее на лист бумаги, а затем присоединил
к приемнику. Оказалось, что такая антенна работает не хуже обычной. И
хотя физические принципы такой антенны не изучены до сих пор, это не
помешало Коэну обосновать собственную компанию и наладить их серийный
выпуск. В данный момент американская фирма "Fractal Antenna
System”разработала антенну нового типа. Теперь можно отказаться от
использования в мобильных телефонах торчащих наружных антенн. Так
называемая фрактальная антенна располагается прямо на основной плате
внутри аппарата. 7. Показать принцип моделирования объектов живой природы.
Для построения фрактального дерева используем программу «Построение
геометрических фракталов», разработанную кафедрой «Информатика» ДГТУ.
Примем длину первоначального отрезка равной 30 см. Зададим угол наклона веток 18o.
Рассчитаем длину полученного отрезка после 8 генераций при длине
первоначального «ствола» равной 30см. При моделировании данного дерева
длина каждого последующего отрезка равна 1/3 длины предыдущего. На 8
шаге имеем:
b1=30,
q=1/3,
b8=b1*(1/3)^(n-1),
b8=0,014см.
Рассмотреть галерею «Геометрические фракталы вокруг нас».
8. Итог урока.
|  З В О Н О К НА У Р О К
З В О Н О К НА У Р О К З В О Н О К НА У Р О К
З В О Н О К НА У Р О К