Урок геометрии в 8 классе «Парад четырехугольников» - ГЕОМЕТРИЯ - МАТЕМАТИКА - МАТЕРИАЛЫ ДЛЯ УЧИТЕЛЯ

Оборудование: учебники «Геометрия 7-9 кл.» Атанасян А.С., таблицы, эмблемы и атрибутика у команд, стенд с кроссвордами, карточки с заданиями на разрезание и составление фигур («Мозаика»), карточки с задачами, бумага, ручки, линейки, ножницы, мел, доска, фигуры четырехугольников, магниты.

Класс делится на 5 команд по числу изучаемых в 8 классе четырехугольников. Каждая команда получает название: «Параллелограмм», «Прямоугольник», «Ромб», «Квадрат» и «Трапеция».
Каждая команда готовит свою атрибутику, свой эпиграф к выступлению, составляет кроссворд, готовит теоретический материал по всей теме и особенно тщательно то, что касается их фигуры, решает задачи (их 25). Задачи даются заранее (за неделю), вывешиваются на стенде. Решение задач сдается учителю перед заключительным уроком. Приглашается жюри, в которое войдут учителя математики школы и учащиеся 10-го класса.

Учитель говорит о важности темы в процессе изучения геометрии, о том, как будет проходить урок, как будет оцениваться каждый ученик и в целом вся команда.

Ой, ты гой еси, весь честной народ, собирайтесь добры молодцы да красны девицы, в школьных кельях ученые, презамученные. Нынче в царстве – государстве Петра-Дубравская школа – зрелище невиданное – урок открытый по геометрии.
Приходите к нам, будем рады всем!
Надевайте наряды парчовые, сапоги да туфли сафьяновые, захватите настроение приподнятое, веселье да задор доброжелательные.
Ну а наше жюри – бояре думные – оценят ваши мысли умные, дадут наставления мудрые и оценку поставят объективную.

Как во той-то во сторонушке математической по прозванью Петра-Дубрава-то, как в великом царстве – государстве геометрическом – Петра-Дубравская средняя школа, как в большом-то семействе многоугольников жил да был вельможа, по прозванью «Параллелограмм». Господин очень важный и довольный собой, т.к. свойства имел превосходные! А как стороны-то его противоположные – равны и параллельны, да и углы-то противоположные тоже равные, диагонали-то делят его на два равных треугольника и сами-то пересекаются в одной точке и делятся-то этой точкой пополам! И свита-то у него была под стать ему!!
И жила-поживала вместе с ним мирно и преспокойно его сестра родная – «Трапеция», мягкая, добрая и терпеливая! Две противоположные-то ее стороны параллельны, а две другие не параллельны. И равняли ее и поправляли ее: и становилась она то равнобедренной, то прямоугольной-то. И поясом-то красивым подпоясывалась. Назывался этот пояс – средней линией. Не спорила она с братцем – подчинялась ему, ведь была она нрава кроткого, да и одинокая, безропотная.
А у «Параллелограмма»-то было три сына – три молодца-красавца. Старший «Прямоугольник» – важный и довольный (как папа) с четырьмя прямыми углами. Зная «цену» себе в жизни – очень заносчив был. Средний – «Ромб» с четырьмя равными сторонами – задиристый и «колючий». Ну а младшенький «Квадрат» - веселый, озорной и, как колобок, увертливый – с равными сторонами и углами.
Получили они в наследство от отца свойства важные и превосходные, но стали и свои свойства иметь – особые: так у «Прямоугольника» выровнялись диагонали, у «Ромба» они не выровнялись, но стали взаимно-перпендикулярными, да и углы-то они стали пополам делить! Ну а «Квадратику» достались все свойства отца своего и братьев старших.
Жили они счастливо, весело и радостно. Задачи решали, кроссворды придумывали и отгадывали, загадки загадывали, песни и стихи сочиняли.

IV. Учитель. А теперь посмотрим и послушаем, как все четырехугольники о себе и своих свойствах расскажут. Слово предоставляется команде «Параллелограмм». (Члены других команд внимательно слушают, готовят замечания и вопросы.)

V. Команда «Параллелограмм». Их одежда: строгий черный костюм – тройка, черный галстук, на голове шапка «Магистра наук».

Учитель: Какие вопросы будут к команде «Параллелограмм»? Какие замечания?

(Выступление команды по тому же плану, что и команда «Параллелограмм»).

VII. Учитель. А теперь немного отдохнем. Задание на преобразование фигур. Даются конверты с заданиями и четырехугольниками.

Задание: Одним разрезом нужно переделать доставшийся четырехугольник в другой равновеликий ему:

Вновь составленные фигуры прикрепляются к магнитной доске магнитами. Выводы делаются жюри.

(Выступление команды по тому же плану, что и предыдущих команд).

Определение, свойства квадрата говорят члены команды. А потом кто-то из членов команды доказывает один из признаков параллелограмма.

Озорные мы девчата
Всем рассказывать начнем,
Что красивее трапеций
Мы фигуры не найдем!

У трапеций-то у наших
Параллельны стороны
Ну а две другие вовсе
Ну не параллельные!

Подпоясались мы лентой –
Средней линией зовем.
Свойство мы ее все знаем
И сейчас о нем споем.

Середины двух сторон
Она соединяет,
А другим двум параллельна –
Это каждый знает.

Ты сложи-ка основанья,
Раздели их пополам…
Вопреки всем упованьям
Среднюю линию даст нам.

XI. Учитель: «А теперь посмотрим, как команды готовы к решению задач».

Капитаны выходят к столу, вытягивают карточку с задачей и команда решает ее. Время ограничено (5-7 мин.) Текст задач прилагается. Решение задач отдается в жюри.

Что называется ромбом?
Если один из углов параллелограмма равен 70о, чему равны другие углы? (110о, 70о, 110о)
Чем отличается прямоугольник от параллелограмма? (Углы по 90о)
Одна из сторон ромба равна 5 см. чему равен его периметр? (20 см.)
Квадрат – … (закончить фразу)
Одна сторона прямоугольника 3 см., другая в 2 раза больше. Чему равен периметр прямоугольника и его площадь? (18 см. и 18 см2.)
В ромбе один из углов его 100о. Чему равен угол между его диагоналями? (90о)
Какая фигура называется параллелограммом?
Существует ли в прямоугольнике точка, равноудаленная и от сторон, и от его вершин? (Да, точка пересечения диагоналей)
В чем сходство ромба и прямоугольника?
У ромба и квадрата равны стороны. У какой фигуры больше периметр? А площадь? (Периметр одинаков, площадь квадрата больше площади ромба)
В чем отличие ромба от прямоугольника?
Если у трапеции два прямых угла, а третий равен 60о, чему равен четвертый угол? (120о)
Как называется трапеция, у которой две боковые стороны равны?
У прямоугольника одна диагональ 10 см. Чему равна половина второй диагонали? (5 см.)
Сколько осей симметрии у 1) параллелограмма; 2) прямоугольника; 3) ромба; 4) квадрата; 5) равнобедренной трапеции? (1) – нет; 2) 2; 3) 2; 4) 4; 5) 1. )
Есть ли центр симметрии у каждой из этих фигур?
В ромбе один из углов равен 60о. Что можно сказать о его меньшей диагонали? (Равна меньшей стороне)
Чем отличается квадрат от ромба?
Чем отличается квадрат от прямоугольника?

Задачи к уроку «Парад четырехугольников»

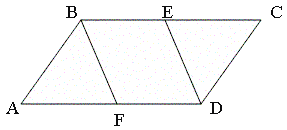
Середины E и F параллельных сторон BC и AD параллелограмма ABCD соединены отрезками с D и B. Доказать, что четырехугольник BEDF – параллелограмм.
В параллелограмме разность двух сторон 3 дм., а периметр его 26 дм. Найти его стороны.
меньшая сторона параллелограмма равна 4 см. Биссектрисы углов, прилежащих к большей стороне, пересекаются в точке, лежащей на противолежащей стороне. Найдите периметр параллелограмма.
В прямоугольнике диагональ образует со стороной угол, равный 36о. Определить угол между диагоналями, обращенный к меньшей стороне.
Стороны прямоугольника относятся между собой, как 1:5. Найти их, если периметр прямоугольника равен 36 см.
Доказать, что любой прямоугольник делится диагоналями на 4 равнобедренных треугольника, попарно равных между собой.
Большой угол между диагоналями прямоугольника равен 110о. Найдите углы между диагональю и стороной прямоугольника.
Найти периметр прямоугольника, если его большая сторона равна 15 см., диагональ 20 см., а угол между диагональю и стороной прямоугольника равен 60о.
В ромбе одна из диагоналей равна стороне. Определить углы ромба.
Определить углы ромба, если один из них в 4 раза больше другого.
В ромбе ABCD биссектриса угла BAC пересекает сторону BC в точке M, а диагональ BD в точке N. Найдите угол ANB, угол AMC = 120о.
Диагонали ромба KMNP пересекаются в точке О. найдите углы треугольника КОМ, если угол MNP = 80о.
Найдите периметр ромба ABCD, если угол В = 120о, а диагональ BD равна 8 см.
Дан квадрат, сторона которого 10 дм., диагональ его служит стороной другого квадрата. Найти диагональ последнего.
В равнобедренной трапеции большее основание равно 2,7 м., боковая сторона равна 1 м., угол между ними 60о. Определить меньшее основание.
В равнобедренной трапеции большее основание равно 2,7 м., боковая сторона равна 1 м., угол между ними 60о. Определить меньшее основание.
В прямоугольной трапеции меньшая боковая сторона 12 дм., а меньший острый угол 30о. Найдите большую боковую сторону.
В трапеции ABCD периметр равен 44 см., боковые стороны равны 10 см. и 12 см. Найдите среднюю линию трапеции.
В равнобедренной трапеции боковые стороны равны по 10 см., большее основание 16 см., а угол при большем основании 60о. Найдите меньшее основание.
Найти среднюю линию трапеции, если ее основания равны 6 см. и 9 см.
В прямоугольной трапеции меньшая боковая сторона 12 см., меньшее основание 7 см., а один из углов трапеции 135о. Найдите ее большее основание.

Четверг, 21.11.2024, 23:50 ОБРАЗОВАТЕЛЬНЫЙ ПОРТАЛ	Приветствую Вас Гость \| Регистрация \| Вход
З В О Н О К НА У Р О К Было бы желание - найдешь на сайте знания!	Вы вошли как Гость \| Группа "Гости" \| RSS Главная \| Мой профиль \| Выход