Цели урока:
- проверить умение выполнять действия с
десятичными дробями устно и письменно; закрепить
и проверить умение решать уравнения и задачи на
десятичные дроби;
- развивать быструю работу мысли, смекалку и
внимательность; развивать интерес к математике.
- воспитывать дружеские отношения в классе и
чувство сопереживания друг другу; развивать
умение высказываться.
Вид урока: обобщение и систематизация
знаний.
Тип урока: урок-олимпиада с
использованием презентации.
Оборудование: таблица с записанными
на ней десятичными дробями, карточки с
уравнениями, карточки с задачами, таблица с
заданием на смекалку, таблица с примерами для
устного счёта.
ХОД УРОКА
1. Организационный момент (3 мин.)
Успокоить и рассадить детей.
Учитель: У нас уже была «Олимпиада по
натуральным числам». Теперь мы изучили
десятичные дроби. Самое время для «Олимпиады по
десятичным дробям». Что-то будет схоже с
прошлой олимпиадой, но многие задания будут
новыми. А самое главное, что все действия, задания
и задачи будут только с десятичными дробями.
Поэтому насколько хорошо вы себя покажете,
зависит от ваших знаний по данной теме. Команды,
как и прошлый раз, будут по рядам. Результат
некоторых заданий напрямую будет зависеть от
собранности всей команды.
2. Разминка – устная работа (3 мин)
Учитель: Любое соревнование
начинается с разминки. Нашей разминкой будет
устный счет. Но в этот раз разминка не будет
влиять на результат соревнований, и задания
будут даны вразброс. Поэтому сейчас самое
главное – не правильно отвечать, а настроиться на
урок.
0,2 · 43
+ 0,4
: 0,3
· 2,05 = 61,5 |
0,54 + 3,06
: 0,2
: 9
– 1,99 = 0,01 |
3,5 · 0,2
+ 1,1
: 2
+ 0,1 = 1 |
Примеры задаются вразброс, чтобы подключить к
работе со всех рядов как можно больше учеников.
3. «Кто быстрее?» (5 мин)
Учитель: Ну, а теперь переходим
непосредственно к соревнованиям. Первое
соревнование будет на скорость. У нас на доске
сейчас откроется таблица чисел. На ней вразброс
записаны десятичные дроби. Ваше задание будет
таким: как можно быстрее найти дробь, подходящую
по условию. Это задание не адресовано какому-то
ряду конкретно, поэтому искать будут все. Кто
находит дробь, поднимает руку и читает ее, говоря,
в каком ряду и в каком столбике она находится, У
остальных будет время исправиться, вдруг кто-то
еще найдет дробь, удовлетворяющую условию.
Каждая находка награждается очком для команды.
Вывешивается или открывается таблица.
| 2,4 |
1.72 |
3.3 |
0,9 |
1,24 |
2,3 |
4 |
2.7 |
2,06 |
2,69 |
| 3 |
1,92 |
0,5 |
2,04 |
0,08 |
4,71 |
2,46 |
4,6 |
2,8 |
1,2 |
| 1,51 |
4,4 |
1,36 |
1,99 |
3,16 |
1 |
4,12 |
1,4 |
4,21 |
2,44 |
| 3,1 |
3,41 |
0,71 |
3.5 |
4,73 |
0,32 |
3,7 |
2,93 |
2,91 |
3,03 |
| 2 |
0,7 |
5 |
3,6 |
1,02 |
2.1 |
3,8 |
4,91 |
2,14 |
4,89 |
Даются поочередно условия. Найти:
– дробь, больше 2,5, но меньше 3;
– самую маленькую дробь, находящуюся в
промежутке от 2 до 3;
– самую большую дробь в промежутке от 1 до 2;
– дробь, в которой одна цифра повторяется
несколько раз.
Надо учесть, что первое и четвертое задания
имеют несколько ответов, это обязательно надо
обыграть. За эти задания можно поставить больше
баллов. Второе и третье задания имеют только один
ответ. Но он может быть не найден. Может быть,
будет предложен ответ, удовлетворяющий условиям,
но неточный, и перебить его никто не сможет. Балл
заносится в копилку тем, чей результат остается
последним. В заключение подсчитываются баллы
команд.
4. «Кто точнее?» (4 + 3 мин)
Учитель: Следующее наше соревнование
позволит узнать, чей ряд точнее. Раздаются
карточки с уравнениями. У каждого своя карточка,
свое уравнение. Его нужно решить не на скорость, а
на точность. Тот, кто решит быстрее, баллов не
получит. Он все равно будет ждать остальных. Но
все равно, время ограничено, на решение дается 4-5
минут. После этого, начиная с первого, ответы
уравнений будут читаться и проверяться. Если
уравнение решено правильно, то балл добавляется,
если ответ неверный, то и балла не будет.
| 1) Решить уравнение: х – 3,243 = 5,1 |
2) Решить уравнение: (9,1 – х) – 2,8 = 2,9 |
3) Решить уравнение: (х – 5,6) : 12 = 3,7 |
| 4) Решить уравнение: (х + 2,1) · 4 = 15,2 |
5) Решить уравнение: 3,4 – 9 · х = 1,6 |
6) Решить уравнение: 8,1 : х – 0,7 = 0,3 |
| 7) Решить уравнение: 12 · х + 14 · х + 4,2 = 12 |
8) Решить уравнение: (9,8 – х) : 9 = 0,7 |
9) Решить уравнение: 4,6 · х + 3,8 · х – 1,6 =
0,5 |
Раздаются карточки. Первая карточка –самая
простая, поэтому она дается слабым ученикам. По
команде ученики начинают решение. После 5 минут
проводится проверка. Каждое уравнение – у трех
участников с разных рядов. Один читает ответ,
другой говорит вслух, правильно или нет, если
неправильно, предлагает свой результат. А у
третьего проверяет преподаватель, при этом
говорит, у кого из участников правильный ответ, а
у кого нет. Для проверки, конечно, надо сделать
шаблон. После проверки всех уравнений
подсчитываются баллы. Если какое-то уравнение
никто не смог решить, его надо разобрать на доске.
Если же ошибся один, или, может быть, двое
учеников, они подходят после урока, или на
следующем уроке уравнение разбирается на доске.
5. «Кто выше?» (10 мин)
Учитель: Теперь пришла пора узнать,
кто выше прыгнет. Для того, чтобы прыгнуть как
можно выше, надо решить задание на смекалку. В
данных примерах надо расставить занятые таким
образом, чтобы равенства были верными. Всего 9
примеров, на каждый ряд по 3. Чтобы прыгнуть
высоко, надо решить все три примера. Решение
меньшего количества означает прыжок ниже.
Отвечают все по очереди: сначала ученик с первого
ряда, затем со второго, а потом –с третьего. На
каждый прыжок дается не более двух попыток.
Значит, если предложено два варианта, и ни один не
является верным, то высота не взята.
–На доске в три столбика записаны примеры:
| 305 + 137 = 31,87 |
231 + 58 = 28,9 |
174 + 244 = 26,14 |
| 13 · 7 = 9,1 |
105 · 6 = 6,3 |
102 · 4 = 40,8 |
| 419 –2,5 = 169 |
375 –1,34 = 3616 |
12 –0,01 = 119 |
Кто первый из ряда поднимет руку, тот отвечает.
Если ответили правильно, значит, первая высота
пройдена. Отвечает второй ряд, затем третий. Если
же ответили неверно, то высота не является
взятой, остается еще одна попытка. Трижды к
одному примеру возвращаться нельзя. Если
какой-то пример в классе не решен, то его
записывают для решения дома. За все три примера,
как за самую большую высоту, дается 5 баллов. Если
не решен один пример, то дается 3 балла. Если же
решен только один пример, то дается 1 балл. В конце
подводятся итоги за данный вид работы и за все
вместе.
6. «Кто сильнее?» (10 мин)
Учитель: Теперь пришла пора узнать,
кто сильнее. В этом нам, как и на прошлой
олимпиаде, поможет решение задач, И пройдет оно
таким образом. Задачи буду на десятичные дроби.
На ряд дается 5 задач разной сложности. Какой
сложности задачу решать, вы будете выбирать сами.
Каждая задача – это этап. Если кто-то из ряда
решил эту задачу, то этап считается пройденным.
Этапы идут с первого по пятый. Первый, второй и
третий этапы дают по три очка каждый.
Четвертый этап дает 4 очка, а пятый – 5 очков.
Сначала всем раздаются карточки с задачами.
Нужно проверить, чтобы каждую задачу решал хотя
бы один человек. После раздачи всех карточек на
решение дается 7 минут. По прошествии этого
времени проверяются ответы. После проверки
ответов всех рядов подсчитываются очки.
1) В вазу положили конфеты двух видов. Найдите
массу смеси конфет, если в ней 3,8 кг конфет
первого вида, а конфет второго вида на 1,5 кг
больше.
2) На трех машинах 14,5т груза. На первой машине
5,2т, а на второй – на 0,8т меньше, чем на первой.
Сколько тонн груза на третьей машине?
3) Груз в 11,2т распределили на две автомашины так,
что на одной из них оказалось на 0,84т больше, чем
на другой. Сколько тонн груза оказалось на каждой
автомашине?
4) Два мотоциклиста движутся в противоположных
направлениях. Скорость одного из них 22км/ч, а
другого – на 4км/ч больше. Какое расстояние будет
между ними через 0,25ч, если сейчас между ними 0,8 км?
5) На пошив пальто ушло в 4 раза больше ткани, чем
на юбку.Сколько метров ткани ушло на пошив
пальто, если на юбку ушло на 2,55 м ткани меньше, чем
на пальто?
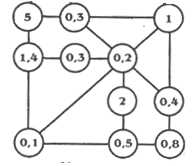
7. «Самый ловкий?» (4 мин)
Учитель: Чтобы узнать, кто самый
ловкий, выполним задание на смекалку. На доске
висит плакат, на нем паутина, связывающая
кружочки с десятичными дробями. Задание такое:
надо с одного угла до другого соединить числа
арифметическими знаками так, чтобы из 0,1
получилась 1. Кто продумал такую комбинацию,
поднимает руку и показывает на доске свое
решение. Если решение верное, то команда
зарабатывает 3 балла.
8. Подведение итогов (3 мин)
Подсчитать баллы и похвалить выигравшую
команду. За активность и дружбу поставить всем
хорошие оценки. Похвалить активных ребят в
каждом ряду. Обсудить с детьми, что они уже умеют
решать хорошо, а что необходимо закрепить. Дать
домашнее задание. Собрать тетради на проверку. В
тетрадях проверяются уравнения и задачи, за что
тоже можно позже выставить оценки. Но главное –
по тетрадям будет видно, с какими уравнениями и
задачами дети справились, а какого типа задания
еще нужно закрепить перед контрольной работой.
Тут же будет видно, справляются ли дети с
оформлением уравнений и задач.
9. Домашнее задание: стр. 138,
«Бесконечное деление» (для тех, кому интересно).
|
 З В О Н О К НА У Р О К
З В О Н О К НА У Р О К З В О Н О К НА У Р О К
З В О Н О К НА У Р О К