Цели урока:
Образовательные:
- Ввести понятие неравенства второй степени с одной переменной, дать определение.
- Построить алгоритм решения неравенств на основе свойств квадратичной функции.
- Сформировать умения решать неравенства данного вида.
Развивающие:
- Выработать умения анализировать, выделять главное, сравнивать, обобщать.
- Формировать графическую и функциональную культуру учащихся.
Воспитательные:
- Показать взаимосвязь математики с окружающей действительностью.
- Формировать навыки общения, умения работать в коллективе.
Тип урока: изучение нового материала.
Оборудование: ПК, проектор, раздаточный материал, интерактивная доска.
Ход урока
I-й этап технологии – вводно-мотивационный.
Ι. Организационный момент.
Здравствуйте, ребята! Садитесь!
Наш урок я хочу начать со слов персидско-таджикского поэта Рудаки:
«С тех пор как существует мирозданье,
Такого нет, кто б не нуждался в знанье.
Какой мы ни возьмем язык и век,
Всегда стремится к знанью человек»
II. Актуализация знаний (фронтальный устный опрос).
Человека отличает от другого живого существа на планете его
неистребимая жажда знаний, тяга к открытиям, созиданию нового. Каждый
урок математики даёт нам этот шанс приобретения новых знаний, умений,
действий, нового вида деятельности. И сегодня вам самим предстоит
открыть новые знания. Но прежде чем совершать открытия, давайте обобщим
те знания, которые у нас есть по математике.
– Какое самое первое математическое понятие у вас было
сформировано? А потом? (Воспитанников нужно вывести на ответы
– Как вы думаете какое из этих понятий является наиболее общим,
широким, где имеют место быть другие оставшиеся? (В ходе диалога
воспитанники должны убедиться в ответе – функция). Перечислите
известные вам функции.(линейная, обратная пропорциональность,
квадратичная, степенная и т.д).Есть функция которая вам известна с 7
класса и свойствами которой вы свободно владеете. Это – линейная
функция! Какие ещё возникают ассоциации со словом линейная – Правильно!
Линейные уравнения и неравенства!
(Вспоминаются алгоритмы решения линейных неравенств и уравнений)
Какая ещё функция была изучена совсем недавно? (квадратичная). Какие
понятия у вас возникают при слове «квадратичная» по аналогии с
линейной функцией? (квадратные уравнения и квадратные неравенства). Что
вы умеете решать из этого, а что нет? Так вот новым умением на уроке и
будет умение решать квадратные неравенства. Но вспомним слова великого
русского физиолога И.П. Павлова.
Проверим как вы усвоили предыдущий материал – свойства квадратичной функции?
При выполнении этого задания какую зависимость мы вспомнили? (Связь
между количеством корней квадратного трёхчлена и нулей функции).
Ребята, для определения промежутков знакопостоянства функции какие
свойства функции нам были нужны? (направление ветвей параболы и нули
квадратичной функции). И записав ответы, мы тем самым что решили?
(Квадратное неравенство ах2+вх+с>0 и <0).
II-й этап – создание ориентировочной основы действий.
IΙΙ. Изложение нового материала.
Итак, тема урока «Решение неравенств второй степени с одной переменной»
А находит ли применение эти неравенства в окружающем нас мире?! А
может это просто прихоть математиков?! Наверно нет! Ведь всякое явление
можно описать с помощью функции, а умения решать неравенства позволяют
ответить на вопрос, при каких значениях аргумента эта функция
положительна, а при каких отрицательна.
Чтобы ответить на этот вопрос нужно вспомнить, что для тел,
брошенных вверх при отсутствии сопротивления воздуха, механика
устанавливает следующее соотношение между высотой подъема тела над
землей(h), начальной высотой тела над землей (h0), начальной скоростью
(v0), ускорением свободного падения (g), углом наклона струи воды α:
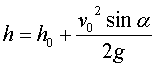
Фонтан смотрится лучше, если капли воды достигают высоты, большей,
чем высота статуи. При высоте каменного цветка фонтана в Москве на ВДНХ
3 м и угле наклона 60º, получим неравенство:
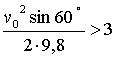
2) Мотоциклист, движущийся по городу со скоростью v0=57 км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением a=12 км/ч2. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением S=v0t+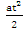 .
Определите наибольшее время, в течение которого мотоциклист будет
находиться в зоне функционирования сотовой связи, если оператор
гарантирует покрытие на расстоянии не далее чем в 30 км от города.
Ответ выразите в минутах. .
Определите наибольшее время, в течение которого мотоциклист будет
находиться в зоне функционирования сотовой связи, если оператор
гарантирует покрытие на расстоянии не далее чем в 30 км от города.
Ответ выразите в минутах.

Итак, сегодня мы будем говорить о квадратных неравенствах, т.е. о
неравенствах второй степени. В рассмотренных примерах неравенств
встречалась одна переменная, но бывают еще неравенства с несколькими
переменными. Сегодня на уроке мы будем рассматривать неравенства второй
степени с одной переменной. Так какие же неравенства мы назовем
неравенствами второй степени с одной переменной?
Даётся определение неравенства второй степени с одной переменной.
Чтобы решить квадратное неравенство достаточно посмотреть на график функции y=ax2+bx+c.
Какие знания о квадратичной функции нам понадобятся для составления
алгоритма решения неравенств? (Воспитанники предлагают различные
варианты). Учитель корректирует и структурирует предложенное.
Затем шаги алгоритма появляются на слайде 12 презентации (алгоритм).
III-й этап технологии – организация "материальной"
предметной деятельности (работа с алгоритмом, схемой решения квадратных
неравенств).
IV. Закрепление: Квадратные неравенства делятся на три типа по количеству
корней квадратного трёхчлена или нулей квадратичной функции.
Итак, квадратные неравенства можно решать применяя алгоритм и
используя свойства квадратичной функции. Но может быть для кого-то
будет понятнее следующий способ:
При решении неравенств может быть один из шести случаев расположения
параболы: если коэффициент а>0, то при решении
использовать:
А если а<0, то умножить обе части неравенства на (-1) изменив при
этом знак неравенства и знак каждого слагаемого на противоположный.
Самостоятельная работа в группах:
1 группа (консультант Попов Антон)
№304(а), 304(е), 315(б)
2 группа (консультант Сергеев Игорь)
№304(в), 304(е), 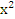 +2х+4>0. +2х+4>0.
3 группа (консультант Баглай Иван)
№304(г), 304(е), 2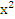 -х+3<0 -х+3<0
4 группа (консультант Деденёв Александр)
№306(а), 306(б), 313(а)
Консультанты оценивают работу подопечных.
V. Рефлексия.
24.11.11 Фамилия Имя ________________
«+» – согласен с утверждением; «–» – не согласен с утверждением.
- Неравенства второй степени с одной переменной решаются с помощью графика квадратичной функции.
- Для решения неравенств второй степени с одной переменной нужно знать координату вершины соответствующей параболы.
- Для решения неравенств второй степени с одной переменной достаточно знать направление ветвей соответствующей параболы.
- Если квадратный трехчлен имеет корни, то соответствующее неравенство обязательно имеет решения.
- Если квадратный трехчлен не имеет корней, то соответствующее неравенство не имеет решений.
- Если вершина параболы лежит на оси абсцисс, то соответствующее неравенство не имеет решений.
- Неравенства второй степени с одной переменной может иметь решение, состоящее из единственного числа.
- Решением неравенства второй степени с одной переменной может быть множество всех чисел.
- Если а<0, х1 и х2 – корни квадратного трехчлена ах2 + bx + c, то решением неравенства ах2 + bx + c> 0 будет промежуток (–∞; х1)
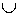 (х2; +∞). (х2; +∞). - Если а>0 и х0– единственный корень квадратного трехчлена ах2 + bx + c, то решением неравенства ах2 + bx + c> 0 будет промежуток (–∞; х0)
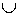 (х0; +∞). (х0; +∞).
«5» – не менее 9 правильных ответов;
«4» – 7, 8 правильных ответов;
«3» – 5, 6 правильных ответов;
«2» – менее 5 правильных ответов.
24.11.11. Фамилия Имя ____________________
- Сегодня на уроке я повторил…
- Сегодня на уроке я узнал …
- Сегодня на уроке я научился…
VI. Домашнее здание.
№ 306(в, г, д, е), 318.Составить задачу, при решении которой является математической моделью квадратное неравенство.
|  З В О Н О К НА У Р О К
З В О Н О К НА У Р О К З В О Н О К НА У Р О К
З В О Н О К НА У Р О К