Термометр

Если привести в соприкосновение два тела, нагретых по-разному, то более нагретое будет охлаждаться, а холодное станет теплее. Про такие два тела говорят, что они обмениваются теплом.

Как уже говорилось, теплообмен - это вид перехода энергии; мы называем более горячим то тело, которое отдает энергию. Мы ощущаем тело горячим, если оно нагревает руку, т. е. передает ей энергию. Наоборот, если тело ощущается холодным, то это значит, оно отнимает энергию у нашего тела.

Про тело, которое отдает тепло (т. е. путем теплообмена отдает энергию), мы говорим: его температура выше температуры того тела, которое забирает это тепло.

Наблюдая за тем, охлаждается или нагревается интересующий нас предмет в присутствии того или иного тела, мы найдем для этого предмета "свое место" в ряду нагретых тел. Температура - это своего рода метка, указывающая, для каких тел интересующий нас предмет будет дарителем, а для каких - получателем тепла.

Температуру измеряют термометрами.

В основу устройства термометров можно положить использование различных свойств тел, чувствительных к температуре. Чаще всего пользуются свойством тел расширяться при повышении температуры.

Если при соприкосновении с разными предметами тело термометра будет изменять свой объем, это значит, что тела имеют разную температуру. Когда объем тела термометра больше - температура выше2 а когда объем меньше - температура ниже.

Самые различные тела могут служить термометрами: и жидкие, как ртуть или спирт, и твердые - металлы, и газообразные. Но ведь разные тела расширяются по-разному, и ртутные, спиртовые, газовые и прочие градусы совпадать не будут. Конечно, всегда можно отметить на всех термометрах две основные точки - температуры таяния льда и кипения воды. Поэтому О и 100 градусов Цельсия все термометры всегда покажут одинаково. Но между 0 и 100 градусами тела будут расширяться не одинаково. Одно тело быстро расширяется между 0 и 50 градусами ртутного термометра и медленно на второй части этого интервала,; а другое - наоборот.

Изготовив термометры с разными расширяющимися телами, мы обнаружим заметные расхождения в их показаниях, несмотря на то, что в основных точках показания будут совпадать. Более того, водяной термометр привел бы нас к такому открытию: если охлажденное до нуля тело положить на электроплитку, то его "водяная температура" сначала бы падала, а потом росла. Это происходит по той причине, что вода при нагревании сначала уменьшает свой объем и лишь потом ведет себя "нормально", т. е. увеличивает объем при нагревании.

Мы видим, что необдуманный выбор вещества для термометра может завести нас в тупик. Но чем же тогда руководствоваться при выборе "правильного" термометра? Какое тело идеально для этой цели?

О таких идеальных телах мы уже говорили. Это идеальные газы. Взаимодействие частиц у идеального газа отсутствует, и, изучая расширение идеального газа, мы изучаем, как меняется движение его молекул. Именно по этой причине идеальный газ является идеальным телом для термометра.

И действительно, сразу бросается в глаза, что если вода расширяется иначе, чем спирт, спирт - иначе, чем стекло, стекло - иначе, чем железо, то водород, кислород, азот или любой другой газ в состоянии разрежения, которого достаточно для того, чтобы заслужить название идеального, расширяются при нагревании в точности одинаково.

Таким образом, основой для определения температуры в физике служит изменение объема определенного количества идеального газа. Разумеется, ввиду сильной сжимаемости газов надо особенно тщательно следить за тем, чтобы газ находился при постоянном давлении.

Для того чтобы проградуировать газовый термометр, мы должны точно измерить объем взятого нами газа при 0°С и при 100°С. Разность объемов V_l00 и V₀ мы разделим на 100 равных частей. Другими словами,

изменение объема газа на 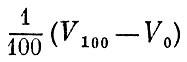и соответствует одному градусу Цельсия (1°С).

Теперь положим, что наш термометр показывает объем V. Какая температура t°C соответствует этому объему? Нетрудно сообразить, что

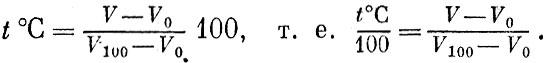
Этим равенством каждый объем V мы относим к температуре t и получаем ту температурную шкалу, которой пользуются в быту.

При увеличении температуры объем газа неограниченно возрастает - нет никакого теоретического предела росту температуры. Напротив, низкие (отрицательные в шкале Цельсия) температуры имеют предел.

Действительно, что произойдет при понижении температуры? Реальный газ в конце концов превратится в жидкость, а при еще большем снижении температуры затвердеет. Молекулы газа соберутся в маленький объем. Но чему будет равен этот объем для нашего термометра, заполненного идеальным газом? Его молекулы не взаимодействуют между собой и не имеют собственного объема. Значит, понижение температуры приведет идеальный газ к нулевому объему. Приблизиться практически сколь угодно близко к поведению, характерному для идеального газа, в данном случае к нулевому значению объема, вполне возможно. Для этого газовый термометр надо заполнять все более и более разреженным газом. Поэтому мы не погрешим против истины, считая предельно малый объем газа равным нулю.

Согласно нашей формуле объему, равному пулю, соответствует самая низкая температура. Эта температура и называется абсолютным нулем температуры.

Для того чтобы определить положение абсолютного нуля на шкале Цельсия, в выведенную формулу температуры надо подставить значение объема, равное нулю, V=0. Таким образом, температура абсолютного нуля равна

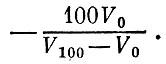
Оказывается, эта замечательная точка соответствует температуре примерно -273°С (точнее,-273,15°С).

Итак, нет температур ниже абсолютного нуля; ведь они соответствуют отрицательным объемам газа. Говорить о более низких температурах бессмысленно. Получить температуры ниже абсолютного нуля так же невозможно, как изготовить проволоку с диаметром меньше нуля.

При абсолютном нуле тело нельзя охладить, т. е. нельзя отнять у него энергию. Иными словами, при абсолютном нуле тела и частицы, из которых они построены, обладают наименьшей возможной энергией. Это означает, что при абсолютном нуле кинетическая энергия равна нулю, а потенциальная имеет наименьшее возможное значение.

Поскольку абсолютный нуль есть самая низкая температура, то естественно, что в физике, особенно в тех ее разделах, где фигурируют низкие температуры, пользуются абсолютной шкалой температур, в которой отсчет ведется от абсолютного нуля. Ясно, что

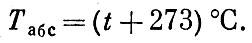
Комнатная температура в абсолютной шкале составляет около 300 градусов. Абсолютную шкалу температур называют также шкалой Кельвина - по имени известного английского ученого XIX века, и вместо обозначения Т_абс употребляют обозначение Т К.

Формула газового термометра, определяющая температуру Т, может быть записана для абсолютной температуры в виде

Пользуясь равенством 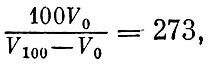приходим к простому результату:

Таким образом, абсолютная температура просто пропорциональна объему идеального газа.

Точные измерения температуры требуют от физика всевозможных ухищрений. В довольно широком интервале температур ртутные, спиртовые (для Арктики) и другие термометры градуируются по газовому термометру. Однако и он непригоден при температурах, весьма близких к абсолютному нулю (ниже 0,7 К), когда все газы сжижаются, а также при температурах выше 600°С, когда газы проникают через стекло. Для высоких и очень низких температур пользуются иными принципами измерения температур.

Что же касается практических способов измерения температуры, то их множество. Большое значение имеют приборы, основанные на электрических явлениях. Сейчас важно запомнить лишь одно: при любых измерениях температуры мы должны быть уверены, что измеряемая величина вполне совпадает с тем, что дало бы измерение расширения разреженного газа.

Высокие температуры возникают в печах и горелках. В кондитерских печах температура достигает 220-280°С. Более высокие температуры применяются в металлургии: 900-1000°С дают закалочные печи, 1400-1500°С - кузнечные. В сталеплавильных печах температура достигает 2000°С.

Рекордно высокие печные температуры получают с помощью электрической дуги (около 5000°С). Пламя дуги позволяет "расправиться" с самыми тугоплавкими металлами.

А какова температура пламени газовой горелки? Температура внутреннего голубоватого конуса пламени всего лишь 300°С. Во внешнем конусе температура доходит до 1800°С.

Несравненно более высокие температуры возникают при взрыве атомной бомбы. По косвенным оценкам, температура в центре взрыва достигает многих миллионов градусов.

В самое последнее время предприняты попытки получить такие сверхвысокие температуры в специальных лабораторных установках, изготовляемых у нас и за рубежом. На кратчайшее мгновение удавалось достигнуть температур в несколько миллионов градусов.

Сверхвысокие температуры существуют и в природе, но не на Земле, а в других телах Вселенной. В центрах звезд, в частности Солнца, температура достигает десятков миллионов градусов. Поверхностные же участки звезд имеют значительно более низкую температуру, не превышающую 20 000 градусов. Поверхность Солнца нагрета до 6000 градусов.

Теория идеального газа

Свойства идеального газа, давшего нам определение температуры,- очень просты. При постоянной температуре действует закон Бойля - Мариотта: произведение pV при изменениях объема или давления остается неизменным. При неизменном, давлении сохраняется частное ^V/_Т, как бы ни менялись объем или температура. Эти два закона легко объединить, Ясно,- что выражение ^pV/_T остается тем же как при постоянной температуре, но изменяющихся V и р, так и при постоянном давлении, но изменяющихся V и Т. Выражение ^pV/_T остается постоянным при изменении не только любой пары, но и одновременно всех трех величин - р, V и Г. Закон ^pV/_Т = const, как говорят, определяет уравнение состояния идеального газа.

Идеальный газ выбран в качестве термометра потому, что толь-- ко его свойства связаны с одним лишь движением (но не с взаимодействием) молекул.

Каков же характер связи между движением молекул и температурой? Для ответа на этот вопрос надо найти связь между давлением газа и движением в нем молекул.

В сферическом сосуде радиуса R заключено N молекул газа (рис. 3.1). Проследим за какой-либо молекулой, например той, что движется в данный момент слева направо вдоль хорды длиной l. На столкновения молекул обращать внимание не будем: такие встречи не сказываются на давлении. Долетев до границы сосуда, молекула ударится о стенку и с той же скоростью (удар упругий) понесется уже в другом направлении. В идеале такое путешествие по сосуду могло бы продолжаться вечно. Если v - скорость молекулы, то каждый удар будет происходить через ^l/_vсекунд, т. е. в секунду каждая молекула ударится ^v/_l раз. Непрерывная дробь ударов N молекул сливается в единую силу давления.

По закону Ньютона сила равна изменению импульса в единицу времени. Обозначим изменение импульса при каждом ударе через Δ. Это изменение происходит ^v/_l раз в секунду. Значит, вклад в силу со стороны одной молекулы будет

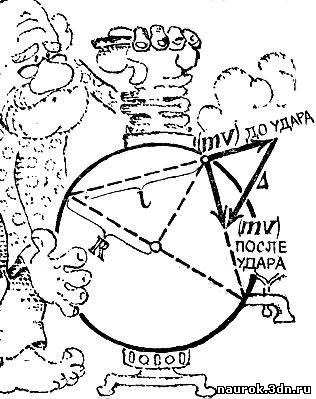
Рис. 3.1

На рис. 3.1 построены векторы импульсов до и после удара, а также вектор приращения импульса Δ. Из подобия возникших при построении треугольников следует: Вклад в силу со стороны одной молекулы примет вид

Так как длина хорды не вошла в формулу, то ясно, что молекулы, движущиеся по любой хорде, дают одинаковый вклад в силу. Конечно, изменение импульса при косом ударе будет меньше, но зато удары в этом случае будут чаще. Расчет показал, что оба эффекта в точности компенсируются.

Так как в сфере N молекул, то суммарная сила будет равна

где v_cp - средняя скорость молекул.

Давление ρ газа, равное силе, деленной на площадь сферы 4πR², будет равно

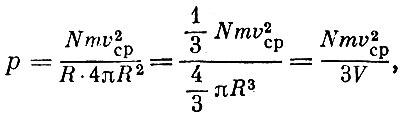
где V - объем сферы.

Таким образом,

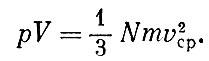
Это уравнение было впервые выведено Даниилом Бернулли в 1738 г.

Из уравнения состояния идеального газа следовало: ρV = const*T; из выведенного уравнения видим, что pV пропорционально v²_cp. Значит,

или

т. е. средняя скорость молекул идеального газа пропорциональна корню квадратному из абсолютной температуры.

Закон Авогадро

Пусть вещество представляет собой смесь различных молекул. Нет ли такой физической величины, характеризующей движение, которая была бы одинакова для всех этих молекул, например для водорода и кислорода, находящихся при одинаковой температуре?

Механика дает ответ на этот вопрос. Можно доказать, что одинаковыми у всех молекул будут средние кинетические энергии поступательного движения ^mv2_ср/₂.

Это означает, что при данной температуре средние квадраты скорости молекул обратно пропорциональны массе частиц:

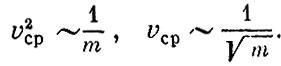
Вернемся теперь к уравнению Так как при данной температуре величины mv²_сp одинаковы для всех газов, то число молекул N, заключенных в данном объеме V при определенных давлении ρ и температуре Т, одинаково для всех газов. Этот замечательный закон был впервые сформулирован Авогадро.

Сколько же молекул приходится на 1 см³? Оказывается, в 1 см³ при 0°С и 760 мм рт. ст. находится 2,7*10¹⁹ молекул. Это огромное число. Чтобы вы почувствовали, сколь оно велико, приведем такой пример. Положим, что газ удаляется из маленького сосудика объемом 1 см³ с такой скоростью, что в каждую секунду уходит миллион молекул. Нетрудно подсчитать, что сосуд полиостью освободится от газа через миллион лет!

Закон Авогадро указывает, что при определенных давлении и температуре отношение числа молекул к объему, в котором они заключены, ^N/_V, есть величина, одинаковая для всех газов.

Так как плотность газа ρ = ^Nm/_V, то отношение плотностей газов равно отношению их молекулярных масс:

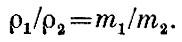
Относительные массы молекул могут быть поэтому установлены простым взвешиванием газообразных веществ. Такие измерения сыграли в свое время большую роль в развитии химии. Из закона Авогадро следует также, что для моля любого вещества, находящегося в состоянии идеального газа, ρV = kN_AT, где к - универсальная постоянная (она носит имя замечательного немецкого физика Людвига Больцмана), равная 1,38.10^-16эрг/_К. Произведение R=kN_A называют универсальной газовой постоянной.

Закон идеального газа записывают часто как

ρV = μRT,

где μ - количество вещества, выраженное в молях. Это уравнение часто используется на практике.

Скорости молекул

Теория указывает, что при одной температуре средние кинетические энергии молекул mv²_ср/2 одинаковы. При нашем определении температуры эта средняя кинетическая энергия поступательного движения молекул газа пропорциональна абсолютной температуре. Комбинируя уравнение идеального газа и уравнение Бернулли, найдем

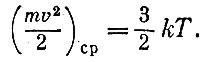
Измерение температуры термометром, заполненным идеальным газом, придает этой мере простой смысл: температура пропорциональна среднему значению энергии поступательного движения молекул. Поскольку мы живем в трехмерном пространстве, про точку, движущуюся как угодно, можно сказать: она имеет три степени свободы. Значит, на одну степень свободы движущейся частицы приходится ^кТ/₂ энергии.

Определим среднюю скорость молекул кислорода при комнатной температуре, которую мы для круглого счета примем в 27°С=300 К. Масса одной молекулы кислорода равна ³²/_(6*10²³₎. Простое вычисление даст м_ср = 4,8*10⁴ см/с, т.е. около 500 м/с. Существенно быстрее движутся молекулы водорода. Их массы в 16 раз меньше и скорости в больше, т. е. при комнатной температуре составляют около 2 км/с. Прикинем, с какой тепловой скоростью движется маленькая? видимая в микроскоп частичка. Обычный микроскоп позволяет увидеть пылинку диаметром в 1 мкм (10^-4 см). Масса такой частицы при плотности,; близкой к единице, будет что-нибудь около 5*10^-13 г. Для ее скорости получим около 0,5 см/с. Неудивительно, что такое движение вполне заметно.

Скорость броуновского движения горошины с массой в 0,1 г будет уже всего только 10^-6 см/с. Немудрено, что мы не видим броуновского движения таких частиц.

Мы говорим о средних скоростях молекулы. Но ведь не все молекулы движутся с одинаковыми скоростями, какая-то доля молекул движется быстрее, а какая-то медленнее. Все это, оказывается можно рассчитать. Приведем только результаты.

При температуре около 15°С, например, средняя скорость молекул азота равна 500 м/с, со скоростями от 300 до 700 м/с движется 59% молекул. С малыми скоростями - от 0 до 100 м/с - движется всего лишь 0,6% молекул. Быстрых молекул со скоростями свыше 1000 м/с в газе всего лишь 5,4% (см. рис. 3.2).

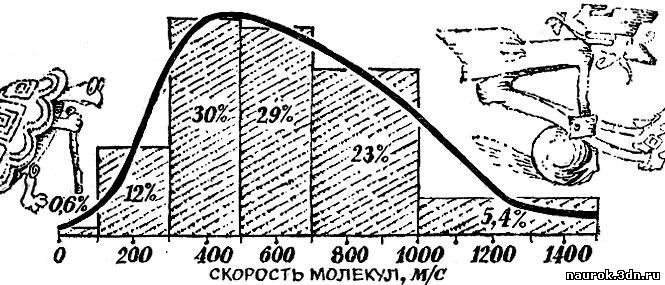
Рис. 3.2

Основание каждого столбика рисунка построено на интервале скоростей, о котором идет речь, а площадь пропорциональна доле молекул, скорости которых лежат в этом интервале.

Можно рассчитать и распределение молекул по разным значениям энергии поступательного движения-

Число молекул энергия которых более чем в два раза превосходит среднюю, уже меньше 10%. Доля еще более "энергичных" молекул тает по мере увеличения энергии во все возрастающей степени. Так, молекул, энергия которых в 4 раза больше средней,- всего 0,7%, в 8 раз больше средней - 0,06*10^-4%, в 16 раз больше средней - 2*10^-8%.

Энергия молекулы кислорода, движущейся со скоростью 11 ^км/_с, равна 23*10^-12 эрг. Средняя энергия молекулы при комнатной температуре равна всего 6*10^-14 эрг. Таким образом, энергия "одиннадцати-километрозой молекулы" по крайней мере в 500 раз больше энергии молекулы со средней скоростью. Неудивительно, что доля молекул со скоростями выше 11 ^км/_с равна невообразимо малому числу - порядка 10^-300.

Но почему нас заинтересовала скорость 11 ^км/_с? В книге 1 мы говорили о том, что оторваться от Земли могут лишь тела, имеющие эту скорость. Значит, забравшись на большую высоту, молекулы могут потерять связь с Землей и отправиться в далекое межпланетное путешествие, но для этого надо иметь скорость 11 ^км/_с. Доля таких быстрых молекул, как мы видим, настолько ничтожна, что опасность потери атмосферы Земле не грозит даже через миллиарды лет.

Скорость ухода атмосферы необычайно сильно зависит от гравитационной энергии γ ^Mm/_r. Если средняя кинетическая энергия молекулы во много раз меньше гравитационной энергии, то отрыв молекул практически невозможен. На поверхности Луны гравитационная энергия в 20 раз меньше, что дает для энергии "убегания" молекулы кислорода значение 1,15*10^-12 эрг. Это значение превышает величину средней кинетической энергии молекулы всего лишь в 20-25 раз. Доля молекул, способных оторваться от Луны, равна 10^-17. Это уже совсем не то, что 10^-300, и подсчет показывает, что воздух будет довольно быстро уходить с Луны в межпланетное пространство. Неудивительно, что на Луне нет атмосферы.

Тепловое расширение

Если нагреть тело, то движение атомов (молекул) будет более интенсивным. Они станут расталкивать друг друга и займут больше места. Этим и объясняется хорошо известный факт: при нагревании твердые, жидкие и газообразные тела расширяются.

О тепловом расширении газов долго говорить не приходится: ведь пропорциональность температуры объему газа была положена в основу нашей температурной шкалы.

Из формулы V = ^V₀/₂₇₃ *Т мы видим, что объем газа при постоянном давлении возрастает при нагревании на 1⁰С на ¹/₂₇₃ часть (т. е. на 0,0037) его объема при 0°С (это положение иногда называют законом Гей-Люссака).

В обычных условиях, т, е. при комнатной температуре и нормальном атмосферном давлении, расширение большинства жидкостей раза в два-три меньше расширения газов.

Мы уже не раз говорили о своеобразии расширения воды. При нагревании от 0 до 4°С объем воды уменьшается с нагреванием. Эта особенность в расширении воды играет колоссальную роль в жизни на Земле. Осенью по мере охлаждения воды верхние остывшие слои становятся плотнее и погружаются на дно. На их место снизу поступает более теплая вода. Но такое перемешивание происходит только до тех пор, пока температура воды не понизится до 4°С. При дальнейшем падении температуры верхние слои уже не будут сжиматься, значит, не будут становиться тяжелее и не станут опускаться на дно. Начиная с этой температуры, верхний слой, постепенно охлаждаясь доходит до нуля градусов и замерзает.

Только эта особенность воды и препятствует промерзанию рек до дна. Если бы вода вдруг потеряла свою замечательную особенность, даже при скромной фантазии легко представить себе бедственные последствия этого.

Тепловое расширение твердых тел существенно меньше, чем тепловое расширение жидкостей. Оно в сотни и тысячи раз меньше расширения газов.

Во многих случаях тепловое расширение является досадной помехой. Так, изменение размеров движущихся частей часового механизма с переменой температуры привело бы к изменению хода часов, если бы для этих тонких деталей не применялся особый сплав-инвар (инвариантный в переводе означает неизменный, отсюда и название "инвар"). Инвар - сталь с большим содержанием никеля - широко применяется в приборостроении. Стержень из инвара удлиняется лишь на одну миллионную долю своей длины при изменении температуры на 1°С.

Ничтожное, казалось бы, тепловое расширение твердых тел может привести к серьезным последствиям. Дело в том, что нелегко мешать тепловому расширению твердых тел из-за их малой сжимаемости.

При нагревании на 1°С стального стержня его длина возрастает всего на одну стотысячную, т. е. на незаметную глазом величину. Однако, чтобы воспрепятствовать расширению и сжать стержень на одну стотысячную, нужна сила в 20 кгс на 1 см². И это только для того, чтобы уничтожить действие повышения температуры всего на 1⁰С!

Распирающие силы, возникающие из-за теплового расширения, могут привести к поломкам и катастрофам, если с ними не считаться. Так, чтобы избежать действия этих сил, рельсы железнодорожного полотна укладывают с зазорами. Об этих силах приходится помнить при обращении со стеклянной посудой, которая легко трескается при неравномерном нагревании. В лабораторной практике поэтому пользуются лишенной этого недостатка посудой из кварцевого стекла (плавленый кварц - окись кремния, находящаяся в аморфном состоянии). При одном и том же нагреве медный брусок удлинится на миллиметр, а такой же брусок кварцевого стекла изменит свою длину на незаметную глазом величину 30-40 мкм. Расширение кварца настолько ничтожно, что кварцевый сосуд можно нагреть на несколько сот градусов, а потом без опасений бросить его в холодную воду.

Теплоемкость

Внутренняя энергия тела, разумеется, зависит от температуры. Чем больше надо нагреть тело, тем больше требуется энергии. На нагрев от Т₁ до Т₂ к телу требуется подвести в виде тепла энергию Q, равную

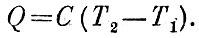
Здесь С - коэффициент пропорциональности, который называется теплоемкостью тела. Из формулы следует определение Понятия теплоемкости: С есть количество тепла, необходимое для повышения температуры на 1°С. Теплоемкость и сама зависит от температуры: нагрев от 0 до 1⁰С, или от 100 до 101⁰С, требует несколько различных количеств тепла.

Величины С относят обычно к единице массы и называют удельными теплоемкостями. Тогда их обозначают строчными буквами с.

Количество тепла, идущее на нагревание тела массы m, запишется формулой

Q = mc(T2-T1).

Мы в дальнейшем будем пользоваться понятием удельной теплоемкости, но для краткости говорить о теплоемкости тел. Дополнительным ориентиром всегда будет размерность величины.

Значения теплоемкостей колеблются в довольно широких пределах. Разумеется, теплоемкость воды в калориях на градус по определению равна 1.

Большинство тел имеет теплоемкость меньше, чем у воды. Так, у большинства масел, спиртов и других жидкостей теплоемкости близки к 0,5 ^кал/_(г*К). Кварц, стекло, песок имеют теплоемкость порядка 0,2. Теплоемкость железа и меди-около О,1 ^кал/_(г*К). А вот примеры теплоемкостей некоторых газов: водород - 3,4 ^кал/_(г*К), воздух - 0,24 ^кал/_(г*К).

Теплоемкости всех тел, как правило, уменьшаются с падением температуры и при температурах, близких к. абсолютному нулю, принимают у большинства тел ничтожные значения. Так, теплоемкость меди при температуре 20 К равна всего 0,0035; это в двадцать четыре раза меньше, чем при комнатной температуре.

Знание теплоемкостей может пригодиться для решения различных задач о распределении тепла между телами.

Различие между теплоемкостями воды и почвы является одной из причин, определяющих разницу между морским и континентальным климатом. Обладая примерно в пять раз большей теплоемкостью, чем почва, вода медленно нагревается и так же медленно остывает.

Летом вода в приморских районах, нагреваясь медленнее чем суша, охлаждает воздух, а зимой теплое море постепенно остывает, отдавая тепло воздуху и смягчая мороз. Нетрудно подсчитать, что 1 м³ морской воды, охлаждаясь на 1°С, нагреет на 1°С 3000 м³ воздуха. Поэтому в приморских районах колебания в температуре и разница между температурой зимы и лета менее значительны, чем в континентальных.

Теплопроводность

Каждый предмет может служить "мостиком", по которому перейдет тепло от тела более нагретого к телу менее нагретому.

Таким мостиком является, например, чайная ложка, опущенная в стакан с горячим чаем. Металлические предметы очень хорошо проводят тепло. Конец ложки в стакане становится теплым уже через секунду.

Если нужно перемешивать какую-либо горячую смесь, то ручку у мешалки надо сделать из дерева или пластмассы. Эти твердые тела проводят тепло в 1000 раз хуже, чем металлы. Мы говорим "проводят тепло", но с таким же успехом можно было бы сказать "проводят холод". Конечно, свойства тела не изменяются от того, в какую сторону идет по нему поток тепла. В морозные дни мы остерегаемся па улице притрагиваться голой рукой к металлу, но без опаски беремся за деревянную ручку.

К плохим проводникам тепла - их также называют теплоизоляторами - относятся дерево, кирпич, стекло, пластмассы. Из этих материалов делают стены домов, печей и холодильников.

К хорошим проводникам относятся все металлы. Наилучшими проводниками являются медь и серебро - они проводят тепло в два раза лучше, чем железо.

Конечно, "мостиком" для перехода тепла может служить не только твердое тело. Жидкости тоже проводят тепло, но. много хуже, чем металлы. По теплопроводности металлы превосходят твердые и жидкие неметаллические тела в сотни раз.

Чтобы показать плохую теплопроводность воды, делают такой опыт. В пробирке с водой закрепляют на дне кусочек льда, а верх пробирки подогревают на газовой горелке - вода начинает кипеть, а лед еще и не думает таять. Если бы пробирка была без воды и из металла, то кусочек льда начал бы таять почти сразу же. Вода проводит тепло примерно в двести раз хуже, чем медь.

Газы проводят тепло в десятки раз хуже, чем конденсированные неметаллические тела. Теплопроводность воздуха в 20 000 раз меньше теплопроводности меди.

Плохая теплопроводность газов позволяет взять в руку кусок сухого льда, температура которого -78°С, и даже держать на ладони каплю жидкого азота, имеющего температуру -196°С. Если не сжимать пальцами эти холодные тела, то "ожога" не будет. Дело заключается в том, что при очень энергичном кипении капля жидкости или кусок твердого тела покрывается "паровой рубашкой" и образовавшийся слой газа служит теплоизолятором.

Сфероидальное состояние жидкости - так называется состояние, при котором капли окутаны паром,- образуется в том случае, если вода попадает на очень горячую сковородку. Капля кипятка, попавшая на ладонь, сильно обжигает руку, хотя разность температур кипятка и человеческого тела меньше разности температур руки и жидкого воздуха. Рука холоднее капли кипятка, тепло уходит от капли, кипение прекращается и паровая рубашка не образуется.

Нетрудно сообразить, что самым лучшим изолятором тепла является вакуум - пустота. В пустоте нет переносчиков тепла, и теплопроводность будет наименьшей.

Значит, если мы хотим создать тепловую защиту; спрятать теплое от холодного или холодное от теплого, то лучше всего соорудить оболочку с двойными стенками и выкачать воздух из пространства между стенками. При этом мы сталкиваемся со следующим любопытным обстоятельством. Если по мере разрежения газа следить за изменением его теплопроводности, то мы обнаружим, что вплоть до того момента, когда давление достигает нескольких миллиметров ртутного столба, теплопроводность практически не меняется и лишь при переходе к более высокому вакууму наши ожидания оправдываются - теплопроводность резко падает.

В чем же дело?

Для того чтобы понять это явление, надо попробовать наглядно представить себе, в чем заключается явление переноса тепла в газе.

Передача тепла от нагретого места в холодные происходит путем передачи энергии от одной молекулы к соседней. Понятно, что соударения быстрых молекул с медленными обычно приводят к ускорению медленных молекул и замедлению быстрых. А это и означает, что горячее место станет холоднее, а холодное нагреется.

Как же сказывается уменьшение давления на передаче тепла? Так как уменьшение давления понижает плотность, уменьшится и число встреч быстрых молекул с медленными, при которых происходит передача энергии. Это уменьшало бы теплопроводность. Однако; с другой стороны, уменьшение давления приводит к увеличению длины свободного пробега молекул,; которые, таким образом, переносят тепло на большие расстояния, а это способствует увеличению теплопроводности. Расчет показывает, что оба эффекта уравновешиваются, и способность к передаче тепла не меняется некоторое время при откачке воздуха.

Так будет до тех пор, пока вакуум не станет настолько значительным, что длина пробега сравняется с расстоянием между стенками сосуда. Теперь дальнейшее понижение давления уже не может изменить длины пробега молекул, "болтающихся" между стенками, падение плотности не "уравновешивается" и теплопроводность быстро падает пропорционально давлению, доходя до ничтожных значений по достижении высокого вакуума. На применении вакуума и основано устройство термосов. Термосы очень распространены, они применяются не только для хранения горячей и холодной пищи, но и в науке и технике. В этом случае их называют, по имени изобретателя, сосудами Дьюара. В таких сосудах (иногда их просто называют дьюарами) перевозят жидкие воздух, азот, кислород. Позже мы расскажем, каким образом эти газы получаются в жидком состоянии.

Конвекция

Но если" вода такой плохой проводник тепла, то как же она нагревается в чайнике? Воздух еще хуже проводит тепло; тогда непонятно, почему во всех частях комнаты зимой устанавливается одинаковая температура.

Вода в чайнике быстро закипает из-за земного притяжения. Нижние слои воды, нагреваясь, расширяются, становятся легче и поднимаются кверху, а на их место поступает холодная вода. Быстрый нагрев происходит лишь благодаря конвекции (латинское слово, означающее "перемешивание"). Нагреть воду в чайнике, находящемся в межпланетной ракете, будет не так-то легко.

Еще об одном случае конвекции воды, не называя этого слова, мы говорили несколько раньше, объясняя, почему реки не промерзают до дна.

Почему батареи центрального отопления помещаются у пола, а форточки делаются в верхней части окна? Пожалуй, удобнее было бы открывать форточку, если бы она была внизу, а батареи, чтобы не мешались - было бы неплохо поместить под потолком.

Если бы мы послушались таких советов, то быстро бы обнаружили, что комната не прогревается батареей и не проветривается при открытой форточке.

С воздухом в комнате происходит то же самое, что и с водой в чайнике. Когда батарея центрального отопления включается, воздух в нижних слоях комнаты начинает нагреваться. Он расширяется, становится легче и поднимается кверху, к потолку. На его место приходят более тяжелые слои холодного воздуха. И они, нагревшись, уходят к потолку. Таким образом в комнате возникает непрерывное течение воздуха - теплого снизу вверх и холодного сверху вниз. Открывая форточку зимой, мы впускаем в комнату поток холодного воздуха. Он тяжелее комнатного и идет вниз, вытесняя теплый воздух, который поднимается кверху и уходит в форточку.

Керосиновая лампа хороню разгорается лишь тогда,; когда на нее надето высокое стекло. Не следует думать, что стекло нужно только для защиты пламени от ветра. И в самую тихую погоду яркость света сразу возрастает, как только на лампу надето стекло. Роль стекла состоит в том, что оно усиливает приток воздуха к пламени - создает тягу. Это происходит по той причине,; что воздух внутри стекла, обедненный кислородом, затраченным на горение, быстро нагревается и идет кверху, а на его место поступает чистый холодный воздух через отверстия, сделанные в горелке лампы.

Чем выше стекло, тем лампа будет лучше гореть. Действительно, быстрота, с которой устремляется холодный воздух в горелку лампы, зависит от разности в весе нагретого столба воздуха в лампе и холодного воздуха вые лампы. Чем выше столб воздуха, тем больше будет эта разность веса, а с ней и быстрота перемешивания.

Поэтому и заводские трубы делают высокими. Для заводских топок нужен особенно сильный приток воздуха, нужна хорошая тяга. Она и достигается благодаря высоким трубам.

Отсутствие конвекции в лишенной тяжести ракете не позволит пользоваться спичками, лампами и газовыми горелками: продукты сгорания задушат пламя!

Воздух - плохой проводник; при его помощи мы можем сохранять тепло, но с одним условием: если мы избежим конвекции - перемешивания теплого и холодного воздуха,- которая сводит на нет теплоизоляционные свойства воздуха.

Устранение конвекции достигается применением разного рода пористых и волокнистых тел. Внутри таких тел воздуху трудно двигаться. Все подобные тела хороши как теплоизоляторы только благодаря способности удерживать слой воздуха. Теплопроводность же самих веществ волокна или стенок пор может быть не очень малой.

Хороша шуба из густого меха, содержащего как можно больше волокон; гагачий пух позволяет изготовлять теплые спальные мешки весом меньше полукилограмма из-за исключительной тонины своих волокон. Полкилограмма этого пуха могут "задержать" столько же воздуха, сколько десяток килограммов ватина.

Для уменьшения конвекции делают двойные рамы. Воздух между стеклами не участвует в перемешивании воздушных слоев, происходящем в комнате.

Наоборот, всякое движение воздуха усиливает перемешивание и увеличивает передачу тепла. Именно поэтому, когда нам нужно, чтобы тепло уходило побыстрее, мы обмахиваемся веером или включаем вентилятор. Но если температура воздуха выше температуры нашего тела, то перемешивание приводит к обратному результату, и ветер ощущается, как горячее дыхание.

Задача парового котла состоит в том, чтобы как можно быстрее получать нагретый до нужной температуры пар. Естественной конвекции в поле тяжести для этого совершенно недостаточно. Поэтому создание интенсивной циркуляции воды и пара, приводящей к перемешиванию теплых и холодных слоев, является одной из основных задач при конструировании паровых котлов.