Силы сопротивления при больших скоростях

Но вернемся к законам "мокрого" трения. Как мы выяснили, при малых скоростях сопротивление зависит от вязкости жидкости, скорости движения и линейных размеров тела. Рассмотрим теперь законы трения при больших скоростях. Но прежде надо сказать, какие скорости считать малыми, а какие большими. Нас интересует не абсолютная величина скорости, а то8 является ли скорость достаточно малой, чтобы выполнялся рассмотренный выше закон вязкого трения.

Оказывается, нельзя назвать такое число метров в секунду, чтобы во всех случаях при меньших скоростях были, применимы законы вязкого трения. Граница применения изученного нами закона зависит от размеров тела и от степени вязкости и плотности жидкости.

Для воздуха "малыми" являются, скорости меньше

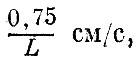
для воды - меньше

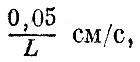
а для вязких жидкостей, вроде густого меда, - меньше

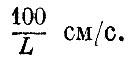
Таким образом, к воздуху и особенно к воде законы вязкого трения мало применимы: даже при малых скоростях, порядка 1 ^см/_с, они будут годиться лишь для крошечных тел миллиметрового размера. Сопротивление, испытываемое ныряющим в воду человеком, ни в какой степени не подчиняется закону вязкого трения.

Чем же объяснить, что при изменении скорости меняется закон сопротивления среды? Причины надо искать в изменении характера обтекания жидкостью движущегося в нем тела. На рис. 6.3 изображены два круговых цилиндра, движущихся в жидкости (ось цилиндра перпендикулярна к чертежу). При медленном движении жидкость плавно обтекает движущийся предмет - сила сопротивления, которую ему приходится преодолевать, есть сила вязкого трения (рис. 6.3, а). При большой скорости позади движущегося тела возникает сложное запутанное движение жидкости (рис. 6.3, б). В жидкости то появляются, то пропадают различные струйки, они образуют причудливы фигуры, кольца, вихри. Карта на струек все время меняется. Появление этого движения, называемого турбулентным, в корне меняет закон сопротивления.

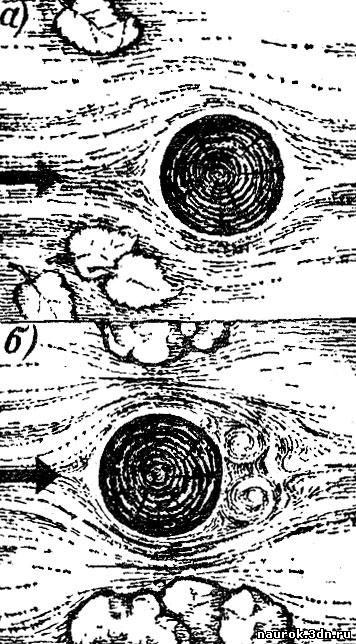
Рис. 6.3

Турбулентное сопротивление зависит от скорости и размеров предмета совсем иначе, чем вязкое: оно пропорционально квадрату скорости и квадрату линейных размеров. Вязкость жидкости при этом движении перестает играть существенную роль; определяющим свойством становится ее плотность,- причем сила сопротивления пропорциональна первой степени плотности жидкости (газа). Таким образом, для силы F турбулентного сопротивления справедлива формула.

F ~ ρν2L2,

где ν - скорость движения, L - линейные размеры предмета и ρ - плотность среды. Числовой коэффициент пропорциональности, который мы не написали, имеет различные значения в зависимости от формы тела.

Обтекаемая форма

Движение в воздухе, как мы говорили выше, почти всегда "быстрое", т. е. основную роль играет турбулентное, а не вязкое сопротивление. Турбулентное сопротивление испытывают самолеты, птицы, парашютисты. Если человек падает в воздухе без парашюта, то через некоторое время он начинает падать равномерно (сила сопротивления уравновешивает вес), но с весьма значительной скоростью, порядка 50 ^м/_с. Раскрывание парашюта приводит к резкому замедлению падения - тот же вес уравновешивается теперь сопротивлением купола парашюта. Так как сила сопротивления пропорциональна скорости движения и размеру падающего, предмета в одинаковой степени, то скорость упадет во столько раз, во сколько изменятся линейные размеры падающего тела. Диаметр парашюта около 7 м, "диаметр" человека около одного метра. Скорость падения уменьшается до 7 ^м/_с. С такой скоростью можно безопасно приземлиться.

Надо сказать, что задача увеличения сопротивления решается значительно легче, чем обратная задача. Уменьшить сопротивление автомобилю и самолету со стороны воздуха или подводной лодке со стороны воды - важнейшие и нелегкие технические задачи.

Оказывается, что, изменяя форму тела, можно уменьшить турбулентное сопротивление во много раз. Для этого надо свести к минимум турбулентное движение, являющееся источником сопротивления. Это достигается приданием предмету специальной, как говорят, обтекаемой формы.

Какая же форма является в этом смысле наилучшей? На первый взгляд кажется, что телу надо придать такую форму, чтобы вперед. двигалось острие. Такое острие, как кажется, должно с наибольшим успехом "рассекать" воздух. Но, оказывается, важно не рассекать воздух, а как можно меньше потревожить его, чтобы он очень плавно обтекал предмет. Наилучшим профилем движущегося в жидкости или газе тела является форма, тупая спереди и острая сзади^[4]. При этом жидкость плавно стекает с острия, и турбулентное движение сводится к минимуму. Ни в коем, случае нельзя направлять острые углы вперед, так как острия вызывают образование турбуленлного движения.

Обтекаемая форма крыла самолета создает не только наименьшее сопротивление движению, но и наибольшую подъемную силу, когда обтекаемая поверхность стоит наклонно вверх к направлению движения. Обтекая крыло, воздух давит на него в основном в направлении, перпендикулярном, к его плоскости (рис. 6.4). Понятно, что для наклонного крыла эта сила направлена вверх.

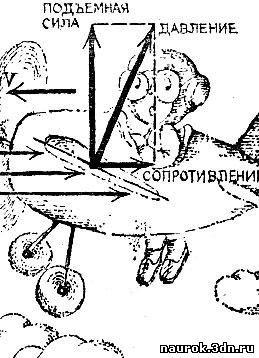
Рис. 6.4

С возрастанием угла подъемная сила -растет. По рассуждение, основанное на одних лишь геометрических соображениях, привело бы нас к неверному выводу, что чем больше угол к направлению движения, тем лучше. На самом же деле по мере увеличения угла плавное обтекание плоскости все затрудняется, а при некотором значении угла, как это иллюстрирует рис. 6.5, возникает сильная турбулентность; сопротивление движению резко возрастает, и подъемная сила падает.

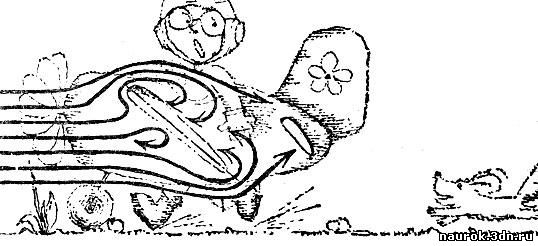
Рис. 6.5

Исчезновение вязкости

Очень часто, объясняя какое-нибудь явление или описывая поведение тех или иных тел? мы ссылаемся на знакомые примеры. Вполне понятно, говорим мы, что этот предмет движется каким-то образом, ведь и другие тела движутся по тем же правилам. Большей частью всегда удовлетворяет объяснение, которое сводит новое к тому, что нам уже встречалось в жизни. Поэтому мы не испытывали особых трудностей, объясняя читателю законы, по которым движутся жидкости,- ведь каждый видела как течет вода, и законы этого движения кажутся вполне естественными.

Однако есть одна совершенно удивительная жидкость, которая не похожа ни на какие другие жидкости, и движется она по особым, только ей свойственным законам. Это жидкий гелий.

Мы уже говорили, что жидкий гелий сохраняется как жидкость при температуре вплоть до абсолютного нуля. Однако гелий выше 2 К (точнее, 2,19 К) и гелий ниже этой температуры -- это совсем разные жидкости. Выше двух градусов свойства гелия ничем не выделяют его среди других жидкостей. Ниже этой температуры гелий становится чудесной жидкостью. Чудесный гелий называют гелием II.

Самое поразительное свойство гелия II - это открытая П. Л. Капицей в 1938 г. сверхтекучесть, т. е. полное отсутствие вязкости.

Для наблюдения сверхтекучести изготовляется сосуд, в дне которого имеется очень узкая щель - шириной всего лишь в полмикрона. Обычная жидкость почти не просачивается сквозь такую щель; так ведет себя и гелий при температуре выше 2,19 К. Но едва только температура становится ниже 2,19 К, скорость вытекания гелия скачком возрастает по крайней мере в тысячи раз. Через тончайший зазор гелий II вытекает почти мгновенно, т. е. полностью теряет вязкость. Сверхтекучесть гелия приводит к еще более странному явлению. Гелий II способен сам "вылезать" из стакана или пробирки, куда он налит. Пробирку с гелием II помещают в дьюаре над гелиевой ванной. "Ни с того ни с сего" гелий поднимается по стенке пробирки в виде тончайшей совершенно незаметной пленки и перетекает через край; с донышка пробирки капают капли.

Надо вспомнить, что благодаря капиллярным силам, о которых говорилось на стр. 36, молекулы всякой жидкости, смачивающей стенку сосуда, взбираются вверх по этой стенке и образуют на ней тончайшую пленку, ширина которой имеет порядок 10^-6 см. Эта пленочка незаметна для глаза, да и вообще ничем себя не проявляет для обычной вязкой жидкости.

Картина совершенно меняется, если, мы имеем дело с лишенным вязкости гелием. Ведь узкая щель не мешает движению сверхтекучего гелия, а тонкая поверхностная пленка - все равно что узкая щель. Лишенная вязкости жидкость течет тончайшим слоем. Через борт стакана или пробирки поверхностная пленка образует сифон по которому гелий переливается через край сосуда.

Понятно, что у обычной жидкости мы не наблюдаем ничего похожего. При. нормальной вязкости "пробраться." через сифон ничтожной толщины жидкость практически не может. Такое движение настолько медленно, что перетекание длилось бы миллионы лет.

Итак, гелий II лишен всякой вязкости. Казалось бы, отсюда с железной логикой следует выв од г что твердое тело должно в такой жидкости двигаться без трения. Поместим в жидкий гелий диск на нити и закрутим нить" Предоставив свободу этому несложному приспособлению, мы создадим нечто вроде маятника - нить с диском будет колебаться и периодически закручиваться то в одну, то в другую сторону. Если трения нет, то мы должны ожидать, что диск будет колебаться вечно. Однако ничего подобного. Через сравнительно короткое время, примерно такое же, как и для обычного нормального гелия I (т. е. гелия при температуре выше 2,19 К), диск останавливается. Что за странность? Вытекая через щель, гелий ведет себя как жидкость без вязкости, а по отношению к движущимся в нем телам ведет себя как обычная вязкая жидкость. Вот это уж действительно совершенно необычно и непонятно.

Нам остается теперь вспомнить сказанное по поводу самого факта, что гелий не затвердевает вплоть до абсолютного нуля. Ведь дело идет о непригодности привычных нам представлений о движении. Если гелий "незаконно" остался жидким, то надо ли удивляться беззаконному поведению этой жидкости.

Понять поведение жидкого гелия можно только с точки зрения новых представлений о движении, которые получили название квантовой механики. Попытаемся дать самое общее представление о том, как квантовая механика объясняет поведение жидкого гелия.

Квантовая механика - очень хитрая и трудная для понимания теория, и пусть читатель не удивляется, что объяснение выглядит еще более странным, чем сами явления. Оказывается, каждая частица жидкого гелия участвует одновременно в двух движениях: одно движение сверхтекучее, не связанное с вязкостью, а другое - обычное.

Гелий II ведет себя таким образом, как будто бы он состоит из смеси двух жидкостей; движущихся совершенно независимо "одна через другую". Одна жидкость нормальна по поведению, т. е. обладает обычной вязкостью, другая составная часть является сверхтекучей.

Когда гелий течет через щель или перетекает через крой стакана, мы наблюдаем эффект сверхтекучести. А при колебании диска, погруженного в гелий, останавливающее диск трение создается благодаря тому, что в нормальной части гелия трение диска неизбежно.

Способность участвовать в двух разных движениях порождает и совершенно необычные теплопроводящие свойства гелия. Как уже говорилось, жидкости вообще довольно плохо проводят тепло. Подобно обычным жидкостям ведет себя и гелий I. Когда же происходит превращение в гелий II, теплопроводность его возрастает примерно в миллиард раз. Таким образом, гелий II проводит тепло лучше, чем самые лучшие обычные проводники тепла - такие, как медь и серебро.

Дело в том, что сверхтекучее движение гелия в передаче тепла не участвует. Поэтому, когда в гелии II есть перепад температур, то возникают два течения, идущие в противоположных направлениях, и одно из них - нормальное - несет с собой тепло. Это совершенно не похоже на обычную теплопроводность. В обычной жидкости тепло передается ударами молекул. В гелии II тепло течет вместе с обычной частью гелияt течет, как жидкость. Вот уж здесь термин "поток тепла" оправдан полностью. Такой способ передачи тепла а приводит к огромной теплопроводности.

Это объяснение теплопроводности гелия может показаться настолько странным, что вы откажетесь в него поверить. Но в справедливости сказанного можно убедиться непосредственно на следующем простом по своей идее опыте.

В ванне с жидким гелием находится дьюар, также полностью заполненный гелием. Сосуд сообщается с ванной капиллярным отростком. Гелий внутри сосуда нагревается электрической спиралью, тепло не переходит к окружающему гелию, так как стенки сосуда не передают тепло.

Напротив капиллярной трубки находится крылышко, подвешенное на тонкой нити. Если тепло течет как жидкость, то оно должно повернуть крылышко. Именно это и происходит. При этом количество гелия в сосуде не изменяется. Как же объяснить это чудесное явление? Лишь единственным способом: при нагревании возникает поток нормальной части жидкости от нагретого места к холодному и поток сверхтекучей части в обратную сторону. Количество гелия в каждой точке не меняется, но так как вместе с переносом тепла движется нормальная часть жидкости, то крылышко поворачивается благодаря вязкому трению этой части и остается отклоненным столько времени, сколько продолжается нагрев.

Из того, что сверхтекучее движение не переносит тепла, следует и другой вывод. Выше говорилось" о "переползании" гелия через край стакана. Но "вылезает" из стакана сверхтекучая часть, а остается нормальная. Тепло связано только с нормальной частью гелия, оно не сопровождает "вылезающую" сверхтекучую часть. Значит, что мере "вылезания" гелия из сосуда одно и то же тепло будет приходиться на все меньшее количество гелия - остающийся в сосуде гелий должен нагреваться. Это действительно наблюдается при опыте.

Массы гелия, связанные с сверхтекучим и нормальным движением, не одинаковы. Отношение их зависит от температуры. Чем ниже температура, тем больше сверхтекучая часть массы гелия. При абсолютном нуле весь гелий становится сверхтекучим. По мере повышения температуры все большая часть гелия начинает вести себя нормально и при температуре 2,19 К весь гелий становится нормальным, приобретает свойства обычной жидкости.

Но у читателя уже вертятся на языке вопросы: что же это за сверхтекучий гелий, как может частица жидкости участвовать одновременно в двух движениях, как объяснить сам факт- двух движений одной частицы?.. К сожалению, мы вынуждены оставить здесь все эти вопросы без ответа. Теория гелия II слишком сложна, и чтобы ее понять, надо знать очень много.

Пластичность

Упругость - это способность тела восстанавливать свою форму после того, как сила перестала действовать. Если к метровой стальной проволоке с поперечным сечением в 1 мм² подвесить килограммовую гирю, то проволока растянется. Растяжение незначительно, всего лишь 0,5 мм, но его нетрудно заметить. Если гирю снять, то проволока сократится на те же 0,5 мм, и метка вернется в прежнее положение. Такая деформация и называется упругой.

Заметим, что проволока сечением в 1 мм² под действием силы в 1 кгс и проволока сечением в 1 см² под действием силы в 100 кгс находятся, как говорят, в одинаковых условиях механического напряжения. Поэтому поведение материала всегда надо описывать, указывая не силу (что беспредметно, если сечение тела неизвестно), а напряжение, т. е. силу, приходящуюся на единицу площади. Обычные тела - металлы, стекло, камни - можно упруго растянуть в лучшем случае всего лишь на несколько процентов. Выдающимися упругими свойствами обладает резина. Резину можно упруго растянуть не несколько сот процентов (т. е. сделать ее вдвое и втрое больше первоначальной длины), а отпустив такой резиновый шнур, мы увидим, что он вернется в исходное состояние.

Все без исключения тела под действием небольших сил ведут себя упруго. Однако предел упругому поведению наступает у одних тел раньше, у других значительно позже. Например, у таких мягких металлов, как свинец, предел упругости наступает уже, если подвесить к концу проволоки миллиметрового сечения груз 0,2-0,3 кгс. У таких твердых материалов, как сталь, этот предел примерно в 100 раз выше, т. е. лежит около 25 кгс.

По отношению к большим силам, превосходящим предел упругости, разные тела можно грубо разделить на два класса - такие, как стекло, т. е. хрупкие, и такие, как глина, т. е. пластичные.

Если прижать палец к куску глины, он оставит отпечаток, в точности передающий даже сложные завитушки рисунка кожи. Молоток, если им ударить по куску мягкого железа или свинца, оставит четкий след. Воздействия нет, а деформация осталась - ее называют пластической или остаточной. Таких остаточных следов не удастся получить на стекле: если упорствовать в этом намерении, то стекло разрушится. Столь же хрупки некоторые металлы и сплавы, например чугун. Железное ведро под ударом молота сплющится, а чугунный котелок расколется. О прочности хрупких тел можно судить по следующим цифрам. Чтобы превратить в порошок кусок чугуна, надо действовать с силой около 50-80 кгс на квадратный миллиметр поверхности. Для кирпича эта цифра падает до 1,5-3 кгс.

Как и всякая классификация, деление тел на хрупкие и пластичные в достаточной степени условно. Прежде всего хрупкое при малой температуре тело может стать пластичным при более высоких температурах. Стекло можно превосходно обрабатывать, как пластический материал, если нагреть его до температуры в несколько сот градусов.

Мягкие металлы, как свинец, можно ковать холодными, но твердые металлы поддаются ковке лишь в сильно нагретом, раскаленном виде. Повышение температуры резко увеличивает пластические свойства материалов.

Одной из существенных особенностей металлов, которые сделали их незаменимыми конструкционными материалами, является их твердость при комнатных температурах и пластичность при высоких: раскаленным металлам легко можно придать требуемую форму, а при комнатной температуре изменить эту форму можно лишь очень значительными силами.

Существенное влияние на механические свойства оказывает внутреннее строение материала. Понятно, что трещины и пустоты ослабляют видимую прочность тела и делают его более хрупким.

Замечательна способность пластически деформируемых тел упрочняться. Одиночный кристалл металла, только что выросший из расплава, очень мягок. Кристаллы многих металлов настолько мягки, что их легко согнуть пальцами, но ... разогнуть такой кристалл не удастся. Произошло упрочнение. Теперь этот образец удастся пластически деформировать лишь существенно большей силой. Оказывается, пластичность есть не только свойство материала, но и свойство обработки.

Почему инструмент готовят не литьем металла, а ковкой? Причина понятна: металл, подвергшийся ковке (или прокату, или протяжке), много прочнее литого. Сколько бы ни ковать металл, мы не сумеем поднять его прочность выше некоторого предела, который называют пределом текучести. Для стали этот предел лежит в интервале 30-50 ^кгс/_мм².

Эта цифра означает следующее. Если на проволоку миллиметрового сечения подвесить пудовую гирю (ниже предела), то проволока начнет растягиваться и одно временно упрочняться. Поэтому растяжение быстро прекратится - гиря будет спокойно висеть на проволоке. Если, же на такой проволоке подвесить двух-трех пудовую гирю (выше предела текучести), то картина будет иной. Проволока будет непрерывно тянуться (течь), пока не разорвется. Еще раз подчеркнем, что механическое поведение тела определяется не силой, а напряжением. Проволока сечением в 100 мкм2 будет течь под действием груза 30-50*10^-4 кгс, т. е. 3-5 гс.

Дислокации

Доказывать, что пластическая деформация - явление, имеющее огромное значение для практики, значит ломиться в открытую дверь. Ковка, штамповка, получение металлических листов, вытягивание проволок - все это явления, имеющие одну природу.

Мы ничего не могли бы понять в пластической деформации, если бы считали, что кристаллиты, из которых построен металл, являются идеальными осколками пространственных решеток.

Теория механических свойств идеального кристалла была создана еще в начале нашего века. Она расходилась с опытом примерно в тысячу раз. Если бы кристалл был идеальным, то его прочность на разрыв должна была бы быть на много порядков выше наблюдаемой и пластическая деформация требовала бы огромных усилий.

Гипотезы зародились ранее, чем накопились факты. Исследователям было очевидно, что единственным выходом, позволяющим примирить теорию и практику, является допущение о наличии у кристаллитов дефектов. Но, конечно, о характере этих дефектов можно было делать самые различные предположения. Лишь тогда, когда физики вооружились тончайшими методами исследования строения вещества, картина стала проясняться. Оказалось, что идеальный кусок решетки (блок) имеет размеры порядка нескольких миллионных долей сантиметра. Блоки дезориентированы в пределах секунд или минут дуги.

К концу двадцатых годов скопилось много фактов, которые привели к важному утверждению, что главным (хотя и не единственным) дефектом реального кристалла является закономерное смещение, получившее название дислокации. Простая дислокация иллюстрируется модельным рис. 6.6. Как видите, сущность дефекта заключается в том, что в кристалле существуют места, содержащие как бы одну "лишнюю" атомную плоскость. Штриховая линия в середине кристалла на рис. 6.6,а разделяет два блока. Верхняя часть кристалла сжата, а нижняя - растянута. Дислокация быстро рассасывается, как это показано на рис. 6.6, б, изображающем вид на левый рисунок "сверху".

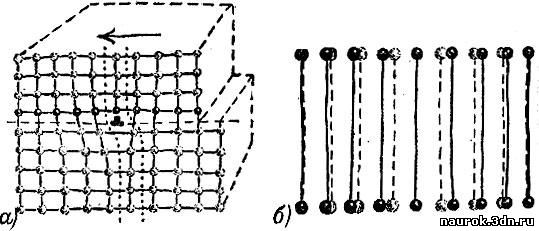
Рис. 6.6

Другие дислокации, которые часто встречаются в кристаллах, называются спиральными. Их схемы показаны на рис. 6.7. Здесь решетка разбита на два блока, один из которых своей частью как бы соскользнул на один период по отношению к соседнему. Наибольшие искажения сосредоточены около оси. Область, примыкающая к этой оси, и называется спиральной дисклока-цией.

Мы лучше поймем, в чем сущность искажения, если рассмотрим схему на том же рисунке, изображающую две соседние атомные плоскости по одну и другую сторону плоскости разреза (рис. 6.7, б). По отношению к трехмерному рисунку это вид на плоскости справа. Ось спиральной дислокации та же, что и на трехмерном рисунке. Сплошными линиями показана плоскость правого, пунктирными - левого блока. Черные точки расположены к читателю ближе, чем белые. Как видно из схемы, спиральная дислокация представляет собой иной тип искажения, отличный от простого. Лишнего ряда атомов здесь нет. Искажение состоит в том; что вблизи "оси дислокации атомные ряды меняют своих ближайших соседей, а именно изгибаются и подравниваются к соседям, находящимся этажом ниже.

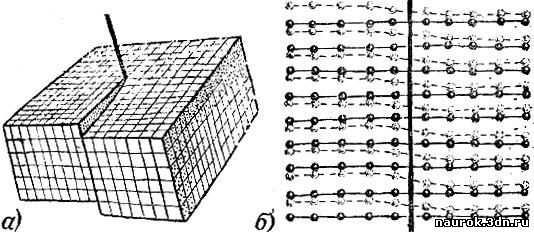
Рис. 6.7

Почему эта дислокация называется спиральной? Представьте себе, что вы шагаете но атомам (предварительно уменьшившись до субатомного размера) и поставили перед собой цель обойти кругом ось дислокации. Нетрудно видеть, что, начав свое путешествие с самой нижней плоскости, вы после каждого оборота будете попадать этажом выше и в конце концов выйдете на верхнюю поверхность кристалла так, как если бы вы шли по спиральной лестнице. На нашем рисунке подъем снизу происходил против часовой стрелки. Если бы сдвиг блоков был обратным, то путешествие происходило бы по часовой стрелке.

Теперь мы подошли к ответу на вопрос о том, как происходит пластическая деформация,

Предположим, что мы хотим сдвинуть верхнюю половинку кристалла по отношению к нижней на одно межатомное расстояние. Вы видите, что для этого придется перекатить друг через друга все ряды атомов, расположенные в плоскости сдвига. Совершенно иначе обстоит дело при действии силы сдвига на кристалл с дислокацией.

На рис. 6.8 показана плотная упаковка шаров (показаны только крайние шары атомных рядов), содержащая простую дисклокацию. Начнем сдвигать вправо верхний блок по отношению к нижнему. Чтобы легче было разобраться в происходящем, мы пометили шары цифрами; шары сжатого слоя помечены цифрами со штрихами. В какой-то исходный момент "трещина" была между рядами 2 и 3; сжатыми были ряды 2' и 3'.

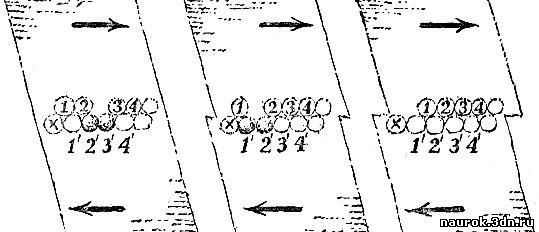
Рис. 6.8

Как только подействует сила, ряд 2 сдвинется в трещину; теперь шар 3' может "вздохнуть свободно", зато придется сжаться шару 1'. Что же произошло? Вся дисклокация передвинулась влево, и ее движение будет таким же образом продолжаться до тех пор, пока дислокация не "выйдет" из кристалла. Результатом будет сдвиг на один ряд атомов, т. е. такой же результат, как при сдвиге идеального кристалла.

Не приходится доказывать, что дислокационный сдвиг требует намного меньшей силы. В первом случае надо преодолеть взаимодействие между атомами - перекатить все атомные ряды; во втором случае в каждый момент перекатывается лишь один единственный ряд атомов.

Прочность кристалла в предположении сдвига без наличия дисклокаций в сто раз больше значения прочности, наблюдаемой на опыте.

Однако возникает следующая трудность. Как это ясно из рисунка, приложенная сила "выгоняет" дислокацию из кристалла. Значит, по мере увеличения степени деформации кристалл должен становиться все прочнее и, наконец, когда последняя из дислокаций будет удалена, кристалл должен достичь, согласно теории, прочности, примерно в сто раз большей прочности идеального правильного кристалла. Кристалл действительно упрочняется по мере увеличения степени деформаций, но далеко не в сто раз. Спасают положение спиральные дислокации. Оказывается (но здесь читатель должен поверить нам на слово, так как очень трудно иллюстрировать это чертежом), спиральные дисклокаций не так-то просто "выгнать" из кристалла. Кроме того, сдвиг кристалла может происходить с помощью дислокаций обоих типов. Теория дислокаций удовлетворительно объясняет особенности явлений сдвига кристаллических плоскостей. Движение беспорядка вдоль кристалла - вот что такое с современной точки зрения представляет собой пластическая деформация кристаллов.

Твердость

Прочность и твердость не идут друг с другом об руку. Веревочный канат, лоскут сукна, шелковая нить могут обладать весьма большой пррчностью - нужно значительное напряжение, чтобы разорвать их. Разумеется, никто не скажет, что веревка и сукно - твердые материалы. И наоборот, прочность стекла невелика, а стекло - твердый материал.

Понятие твердости, которым пользуются в технике, заимствовано из житейской практики. Твердость - это противодействие внедрению. Тело твердое, если его трудно процарапать, трудно оставить на нем отпечаток. Определения эти могут показаться читателю несколько туманными. Мы привыкли к тому, что физическое понятие выражают числом. Как же это сделать в отношении твердости?

Один весьма кустарный, но в то же время практически полезный способ уже давно используется минерологами. Десять определенных минералов располагают в ряд. Первым стоит алмаз, за ним следует корунд, далее - топаз, кварц, полевой шпат, апатит, плавиковый шпат, известковый шпат, гипс и тальк. Ряд подобран следующим образом: алмаз оставляет царапину на всех минералах, но ни один из этих минералов, не может процарапать алмаз. Это и значит, что алмаз самый твердый минерал. Твердость алмаза оценивается числом 10. Следующий в ряду за алмазом корунд тверже всех других нижестоящих минералов - корунд может их процарапать. Корунду присваивают число твердости 9. Числа 8, 7 и 6 присвоены соответственно топазу, кварцу и полевому шпату на тех же основаниях.

Каждый из них тверже (т. е. может нанести царапину), чем все нижестоящие минералы, и мягче (сам может быть процарапан) минералов, имеющих большие числа твердости. Самый мягкий минерал - тальк - имеет одну единицу твердости.

"Измерение" (приходится это слово брать в кавычки) твердости при помощи этой шкалы заключается в нахождении места интересующего нас минерала в ряду десяти выбранных стандартов.

Если неизвестный минерал можно процарапать кварцем, но сам он оставляет царапину на полевом шпате, то его твердость равна 6,5.

Металловеды пользуются другим способом определения твердости. Стандартной силой (обычно 3000 кгс) при помощи стального шарика диаметром в 1 см на испытуемом материале делается вмятина. Радиус образовавшейся ямки принимается за число твердости.

Твердость по отношению к царапанию и твердость по отношению к вдавливанию не обязательно сочетаются, и один материал может оказаться тверже другого при испытании на царапание, но мягче при испытании на вдавливание.

Таким образом, нет универсального понятия твердости, не зависящего от способа измерения. Понятие твердости относится поэтому к техническим, но не к физическим понятиям.

Звуковые колебания и волны

Мы уже сообщили читателю много сведений о колебаниях, Как колеблется маятник, шарик на пружинке, каковы закономерности колебания струны - этим вопросам была посвящена одна из глав книги 1. Мы не говорили о том, что происходит в воздухе или другой среде, когда находящееся в ней тело совершает колебания. Не вызывает сомнения, что среда не может остаться равнодушной к колебаниям. Колеблющийся предмет толкает воздух, смещает частицы воздуха из тех положений, в которых они находились ранее. Понятно также что дело не может ограничиться влиянием лишь на близлежащий слой воздуха. Тело сожмет ближайший слой, этот слой давит на следующий - и так слой за слоем, частица за частицей приводится в движение весь окружающий воздух. Мы говорим, что воздух пришел в колебательное состояние или что в воздухе происходят звуковые колебания.

Мы называем колебания среды звуковыми, но это не значит, что все звуковые колебания мы слышим. Физика пользуется понятием звуковых колебаний в более широком смысле. Какие звуковые колебания мы слышим - об этом будет рассказано ниже.

Речь идет о воздухе лишь потому, что звук чаще всего передается через воздух. Но, разумеется, нет никаких особых свойств у воздуха, чтобы за ним оказалось монопольное право совершать звуковые колебания. Звуковые колебания возникают в любой среде, способной сжиматься, а так как несжимающихся тел в природе нет, то, значит, частицы любого материала могут оказаться в этих условиях. Учение о таких колебаниях обычно называют акустикой.

При звуковых колебаниях каждая частица воздуха в среднем остается на месте - она совершает лишь колебания около положения равновесия. В самом простейшем случае частица воздуха может совершать гармоническое колебание, которое, как мы помним, происходит по закону синуса. Такое колебание характеризуется максимальным смещением от положения равновесия - амплитудой и периодом колебания, т. е. временем, затрачиваемым на совершение полного колебания.

Для описания свойств звуковых колебаний чаще пользуются понятием частоты колебания, нежели периодом. Частота v = ¹/_T есть величина, обратная периоду. Единица частоты - обратная секунда (с^-1), однако такое слово не распространено. Говорят - секунда в минус первой степени или герц (Гц). Если частота колебания равна 100 с^-1, то это значит, что за одну, секунду частица воздуха совершит 100 полных колебаний. Так как в физике весьма часто приходится иметь дело с частотами, которые во много раз больше герца, то имеют широкое применение единицы килогерц (1 кГц = 10³ Гц) и мегагерц (1 МГц = 10⁶ Гц).

При прохождении равновесного положений скорость колеблющейся частицы максимальна. Напротив, в положениях крайних смещений скорость частицы, естественно, равняется нулю. Мы уже говорили, что если смещение частицы подчиняется закону гармонического колебания, то и изменение скорости колебания следует тому же закону. Если обозначить амплитуду смещения через s₀, а амплитуду скорости через v₀, то v₀ = ^2πs₀/_T иди ν⁰ = 2πvs₀. Громкий разговор приводит частицы воздуха в колебание с амплитудой смещения всего лишь в несколько миллионных долей сантиметра. Амплитудное значение скорости будет величиной порядка 0,02 см/с.

Другая важная физическая величина, колеблющаяся вместе со смещением и скоростью частицы,- это избыточное давление, называемое также звуковым. Звуковое колебание воздуха состоит в периодическом чередовании сжатия и разрежения в каждой точке среды. Давление воздуха в любом месте то больше, то меньше давления, которое было при отсутствии звука. Этот избыток (или недостаток) давления и называется звуковым. Звуковое давление составляет совсем небольшую долю нормального давления воздуха. Для нашего примера - громкий разговор - амплитуда звукового давления будет равна примерно миллионной доле атмосферы. Звуковое давление прямо пропорционально скорости колебания частицы, причем отношение этих физических величин зависит только от свойств среды. Например, звуковому давлению в воздухе в 1 дин/см² соответствует скорость колебания 0,025 ^см/_с.

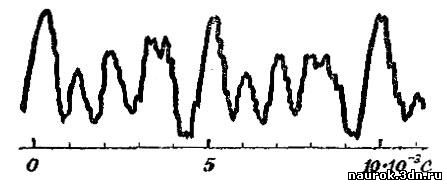
Рис. 6.9

Струна, колеблющаяся по закону синуса, приводит и частицы воздуха в гармоническое колебание. Шумы и музыкальные аккорды приводят к значительно более сложной картине. На рис. 6.9 показана запись звуковых колебаний, а именно звукового давления в зависимости от времени. Эта кривая мало похожа на синусоиду. Оказывается, однако, что любое сколь угодно сложное колебание может быть представлено как результат наложения одной на другую большого числа синусоид с разными амплитудами и частотами. Эти простые колебания, как говорят, составляют спектр сложного колебания. Для простого примера такое сложение колебаний показано на рис. 6.10.

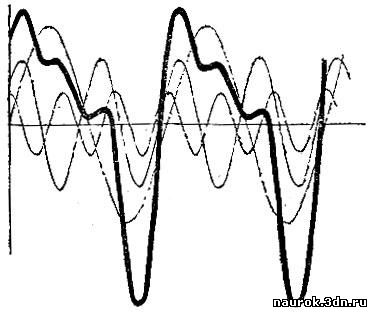
Рис. 6.10

Если бы звук распространялся мгновенно, то все частицы воздуха колебались бы, как одна. Но звук распространяется не мгновенно, и объемы воздуха, лежащие на линии распространения, приходят в движение по очереди, как бы подхватываются волной, идущей от источника. Так же точно щепка лежит спокойно на воде до тех пор, пока круговые водяные волны от брошенного камешка не подхватят ее и не приведут в колебание.

Остановим наше внимание на одной колеблющейся частице и сравним ее поведение с движением других частиц, лежащих на той же линии распространения звука. Соседняя частица придет в колебание немного позже, следующая - еще позже. Запаздывание будет нарастать, пока, наконец, мы не встретимся с частицей, отставшей на целый период и поэтому колеблющейся в такт с исходной. Так отставший на целый круг неудачный бегун может пройти линию финиша одновременно с лидером. На каком же расстоянии встретим мы точку, колеблющуюся в такт с исходной? Нетрудно сообразить, что это расстояние λ равно произведению скорости распространения звука с на период колебания Т. Расстояние λ называется длиной волны:

λ = cT.

Через промежутки λ мы будем встречать колеблющиеся в такт точки. Точки, находящиеся на расстоянии ^λ/₂, будут совершать движение одна по отношению к другой, как предмет, колеблющийся перпендикулярно к зеркалу, по отношению к своему изображению.

Если изобразить смещение (или скорость, или звуковое давление) всех точек, лежащих на линии распространения гармонического звука, то получится опять синусоида.

Не следует путать графики волнового движения и колебаний. Рис. 6.11 и 6.12 очень похожи, но на первом по горизонтальной оси отложено расстояние, а на втором - время. Один рисунок представляет собой временную развертку колебания, а другой - мгновенную "фотографию" волны. Из сопоставления этих рисунков видно, что длина волны может быть названа также ее пространственным периодом: роль Т во времени играет в пространстве величина λ.

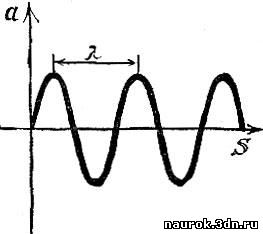
Рис. 6.11

На рисунке звуковой волны смещения частицы отложены по вертикали, а направлением распространения волны, вдоль которого отсчитывается расстояние, является горизонталь. Это может навести на неверную мысль, что частицы смещаются перпендикулярно к направлению распространения волны. В действительности частицы воздуха всегда колеблются вдоль направления распространения звука. Такая волна называется продольной.

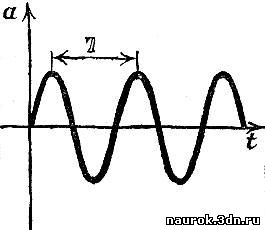
Рис. 6.12

Свет распространяется несравненно быстрее, чем звук,- практически мгновенно. Гром и молния происходят в один и тот же момент, но молнию мы видим в момент ее возникновения, а звук грома доходит до нас со скоростью примерно один километр за три секунды (скорость звука в воздухе составляет 330 ^м/_с). Значит когда слышен гром, опасность удара молнии уже миновала.

Зная скорость распространения звука, обычно можно определить, как далеко проходит гроза. Если от момента вспышки молнии до раската грома прошло 12 с, значит, гроза от нас за 4 км.

Скорость звука в газах примерно равна средней скорости движения молекул газа. Она также зависит от плотности газа и пропорциональна корню квадратному из абсолютной температуры. Жидкости проводят звук быстрее, чем газы. В воде звук распространяется со скоростью 1450 ^м/_с, т. е. в 4,5 раза быстрее, чем в воздухе. Еще больше скорость звука в твердых телах, например, в железе - около 6000 ^м/_с.

Когда звук переходит из одной среды в другую, меняется скорость его распространения. Но одновременно происходит и другое интересное явление - частичное отражение звука от границы между двумя средами. Какая доля звука отразится - это зависит главным образом от соотношения плотностей. В случае падения звука из воздуха на твердые или жидкие поверхности или, наоборот, из плотных сред в воздух звук отражается почти полностью. Когда звук попадает в воду из воздуха или, наоборот, из воды в воздух, то во вторую среду проходит всего лишь ¹/₁₀₀₀ силы звука. Если обе среды плотные, то отношение между проходящим и отраженным звуком может быть и невелико. Например, из воды в сталь или из стали в воду пройдет 13%, а отразится 87% звука.

Явление отражения звука широко применяется в навигации. На нем основано устройство прибора для измерения глубины - эхолота. У одного борта корабля под водой помещают источник звука (рис. 6.13). Отрывистый звук создает звуковые лучи, которые проберутся сквозь водяную толщу ко дну моря или реки, отразятся от дна, и часть звука вернется на корабль, где ее улавливают чувствительные приборы. Точные часы укажут, сколько времени понадобилось звуку на это путешествие. Скорость звука в воде известна, и простым вычислением можно получить точные сведения о глубине.

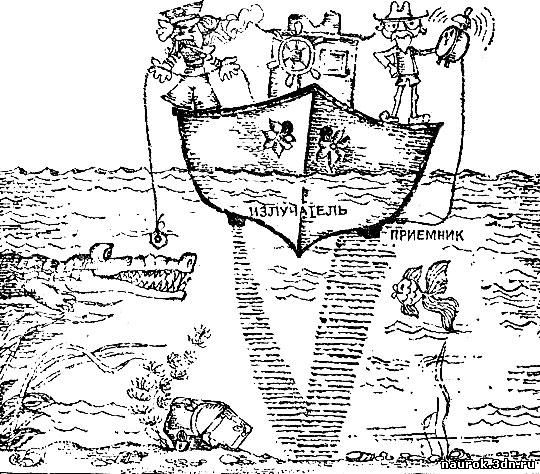
Рис. 6.13

Направляя звук не вниз, а вперед или в стороны, можно при его помощи определить, нет ли около корабля опасных подводных скал или глубоко погруженных в воду айсбергов. Все частицы воздуха, окружающего звучащее тело, находятся в состоянии колебания. Как мы выяснили в книге 1, колеблющаяся по закону синуса материальная точка обладает определенной и неизменной полной энергией.

Когда колеблющаяся точка проходит положение равновесия, скорость ее максимальна. Так как смещенные точки в это мгновение равняется нулю, то вся энергия сводится к кинетической:

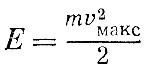
Следовательно, полная энергия пропорциональна квадрату амплитудного значения скорости колебания.

Это верно и для частиц воздуха, колеблющихся в звуковой волне. Однако частица воздуха - это нечто неопределенное. Поэтому энергию звука относят к единице объема. Эту величину можно назвать плотностью звуковой энергии.

Так как масса единицы объема есть плотность ρ, то плотность звуковой энергии

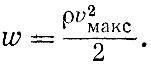
Мы говорили выше еще об одной важной физической величине, совершающей колебания по закону синуса с той же частотой, что и скорость. Это - звуковое или избыточное давление. Так как эти величины пропорциональны, то можно сказать, что плотность энергии пропорциональна квадрату амплитудного значения звукового давления.

Амплитуда скорости звукового колебания при громком разговоре равняется 0,02 ^см/_с. 1 см³ воздуха весит около 0,001 г. Таким образом, плотность энергии равняется

1/2 *10-3 * (0,02)2 эрг/см3 = 2*10-7 эрг/см3.

Пусть колеблется источник звука. Он изучает звуковую энергию в окружающий воздух. Энергия как бы "течет" от звучащего тела. Через каждую площадку, расположенную перпендикулярно к линии распространения звука, за секунду протекает определенное количество энергии. Эта величина называется потоком энергии, прошедшим через площадку. Если, кроме того, взята площадка в 1 см², то протекшее количество энергии называют интенсивностью звуковой волны.

Нетрудно видеть, что интенсивность звука I равна произведению плотности энергии w на скорость звука с. Представим цилиндрик высотой 1 см и площадью основания 1 см², образующие которого параллельны направленно распространения звука. Содержащаяся внутри такого цилиндра энергия w будет полностью покидать его через время ¹/_с. Таким образом, через единицу площади за единицу времени пройдет энергия ^w/₍¹_/c), т. е. wc. Энергия как бы сама движется со скоростью звука.

При громком разговоре интенсивность звука вблизи собеседников будет примерно равна (мы воспользуемся числом, полученным выше)

2*10-7*3*104 = 0,006 эрг/(см2*с).

Слышимый и неслышимый звуки

Какие же звуковые колебания воспринимаются человеком на слух? Оказывается, ухо способно воспринимать лишь колебания, лежащие примерно в интервале от 20 до 20 000 Гц. Звуки с большой частотой мы называем высокими, с малой частотой - низкими.

Какие же длины волн соответствуют предельным слышимым частотам? Так как скорость звука примерно равна 300 ^м/_с, то по формуле λ = cT = ^c/_v находим, что длины слышимых звуковых волн лежат в пределах от 15 м для самых низких тонов до 1,5 см для самых высоких.

Каким же образом мы "слышим" эти колебания?

Работа нашего органа слуха до сих пор не выяснена до конца. Дело в том, что во внутреннем ухе (в улитке - канале длиной несколько сантиметров, заполненном жидкостью) имеется несколько тысяч чувствительных нервов, способных воспринимать звуковые колебания, передающиеся в улитку из воздуха через барабанную перепонку. В зависимости от частоты тона сильнее всего колеблется та или иная часть улитки. Хотя чувствительные нервы расположены вдоль улитки так часто, что возбуждается сразу большое их число, человек (и животные) способен - особенно в детстве - различать изменения частоты на ничтожные (тысячные) ее доли. Каким образом это происходит, до сих пор точно не известно. Ясно только, что важнейшую роль здесь играет анализ в мозгу раздражений, приходящих от множества отдельных нервов. Придумать механическую модель, которая - при той же конструкции - столь же хорошо различала бы частоту звука, как и ухо человека, пока еще не удалось.

Частота звука в 20 000 Гц является пределом, выше которого человеческое ухо не воспринимает механические колебания среды. Различными способами можно создать колебания более высокой частоты, человек их не услышит, но приборы смогут записать. Впрочем, не только приборы фиксируют такие колебания. Многие животные, например летучие мыши, пчелы, киты и дельфины (как видно, дело не в размерах живого существа), способны воспринимать механические колебания с частотой вплоть до 100 000 Гц.

Сейчас удается получать колебания с частотой вплоть до миллиарда герц. Такие колебания, хотя они и неслышимы, называют ультразвуковыми, чтобы подтвердить их родственность звуку. Ультразвуки наибольших частот получают при помощи кварцевых пластинок. Такие пластины вырезаются из монокристаллов кварца.