Многие думают, что кристаллы - это красивые, редко встречающиеся камни. Они бывают разных цветов, обычно прозрачные и, что самое замечательное, обладают красивой правильной формой. Чаще всего кристаллы представляют собой многогранники стороны (грани) их идеально плоские," ребра строго прямые. Они радуют глаз чудесной игрой света в гранях, удивительной правильностью строения.

Есть среди них скромные кристаллы каменной соли - природного хлористого натрия, т. е. обычной поваренной соли. Они встречаются в природе в виде прямоугольных параллелепипедов или кубиков. Простая форма и у кристаллов кальцита - прозрачных косоугольных параллелепипедов. Куда сложнее кристаллы кварца. У каждого кристаллика множество граней разной формы, пересекающихся по ребрам разной длины.

Однако кристаллы - совсем не музейная редкость. Кристаллы окружают нас повсюду. Твердые тела, из которых мы строим дома и делаем станки, вещества, которые мы употребляем в быту,- почти все они относятся к кристаллам. Почему же мы этого не видим? Дело в том, что в природе редко попадаются тела в виде отдельных одиночных кристаллов (или, как говорят, монокристаллов). Чаще всего вещество встречается в виде прочно сцепившихся кристаллических зернышек уже совсем малого размера - меньше тысячной доли миллиметра. Такую структуру можно увидеть лишь в микроскоп.

Тела, состоящие из кристаллических зернышек, называются мелкокристаллическими, или поликристаллическими ("поли"-по-гречески "много").

Конечно, к кристаллам надо отнести и мелкокристаллические тела. Тогда окажется, что почти все окружающие пас твердые тела - кристаллы. Песок и гранит, медь и железо, салол, продающийся в аптеке,; и краски - все это кристаллы.

Есть и исключения; стекло и пластмассы не состоят из кристалликов. Такие твердые тела называются аморфными.

Итак, изучать кристаллы- это значит изучать почти все окружающие нас тела. Понятно, как это важно.

Одиночные кристаллы сразу же узнают по правильности форм. Плоские грани и прямые ребра являются характерным свойством кристалла; правильность формы несомненно связана с правильностью внутреннего строения кристалла. Если кристалл в каком-то направлении особо вытянулся, значит, и строение кристалла в этом направлении какое-то особенное.

Но представьте себе, что из крупного кристалла на станке изготовлен шар. Удастся ли сообразить, что в руках у нас кристалл, и отличить этот шар от стеклянного? Поскольку разные грани кристалла развиты в различной степени, то это наводит на мысль о том, что и физические свойства кристалла неодинаковы в разных направлениях. Сказанное относится к прочности, электропроводности, да и вообще ко многим свойствам. Эта особенность кристалла называется анизотропией его свойств. Анизотропный - это значит разный в разных направлениях.

Кристаллы анизотропны. Напротив, аморфные тела, жидкости и газы изотропны ("изо" - по-гречески "одинаково", "тропос" -- направление), т. е. обладают одинаковыми свойствами в разных направлениях. Анизотропия свойств и позволяет узнать,( является ли прозрачный бесформенный кусочек вещества кристаллом или нет.

Отправимся в минералогический музей и внимательно рассмотрим разные монокристаллические образцы кристаллов одного и того же вещества. Вполне возможно, что на стенде будут выставлены образцы и правильной и неправильной формы. Некоторые кристаллы будут выглядеть как обломки,- другие будут иметь 1-2 грани "ненормального" развития.

Отберем из общей кучи образцы, которые покажутся нам идеальными, и зарисуем их. Картинка, которая получится, показана на рис. 2.6. В качестве примера выбран все тот же кварц. У кварца, как и у других кристаллов, может развиться разное число граней одного "сорта", а также разное число самих "сортов" граней. Пусть внешнее сходство не бросается в глаза, все же такие кристаллики похожи друг на друга, как близкие родственники, как близнецы. В чем же заключается их сходство?

Рис. 2.6

Посмотрите на рис. 2.6, где изображен ряд кристаллов кварца. Все эти кристаллики - близкие "родственники". Их можно сделать и совсем одинаковыми, сошлифовывая грани на различную глубину параллельно самим себе. Легко видеть, что таким способом, например, кристалл II может быть сделан совершенно таким же, как кристалл I. Это возможно потому, что углы между сходственными гранями образцов одинаковы" например, между гранями А и Б, Б и В и т. д.

В этом равенстве углов и заключается "семейное" сходство кристаллов. При сошлифовывании граней параллельно самим себе форма кристалла изменяется, но углы между гранями сохраняют свое значение.

При росте кристалла в зависимости от ряда случайностей одни грани могут попасть в условия более благоприятные, другие в менее удобные для увеличения своих размеров. Внешнее сходство выросших в разных условиях образцов станет незаметным, но углы между сходственными гранями всех кристаллов изучаемого вещества будут всегда одинаковы. Форма кристалла случайна, а углы между гранями отвечают (вы дальше поймете, почему) его внутренней природе.

Но плоскогранность не является единственным свойством кристаллов, которое отличает их от бесформенных тел. Кристаллы обладают симметрией. Смысл этого слова лучше всего мы поймем на примерах.

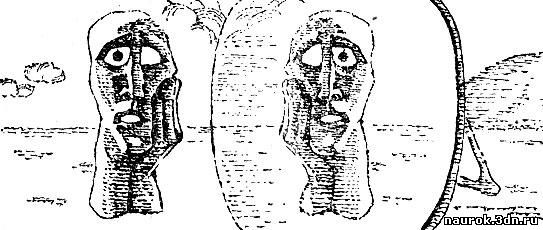
Рис. 2.7

На рис. 2.7 изображена скульптура; перед ней стоит большое зеркало. В зеркале возникает отражение, в точности повторяющее предмет. Скульптор может изготовить две фигуры и расположить их так же, как фигуру и ее отражение в зеркале. Эта "двойная" скульптура будет симметричной фигурой - она состоит из двух зеркально равных частей. Правая часть скульптуры в точности совпадает с отражением левой ее части. Такая симметричная фигура обладает вертикальной плоскостью зеркальной симметрии, которая проходит посередине между ними. Плоскость симметрии -o мысленная плоскость, но мы ее отчетливо ощущаем, рассматривая симметрично построенное тело.

Плоскостью симметрии обладают тела животных, вертикальную плоскость внешней симметрии можно провести через человека. В животном мире симметрия осуществляется лишь приблизительно, да и вообще идеальной симметрии в жизни не существует. Архитектор может изобразить на чертеже дом, состоящий из двух идеально симметричных половин. Но когда дом будет построен, как бы хорошо его ни делали, всегда можно найти разницу в двух соответствующих частях здания; скажем, в одном месте есть трещинка, а в другом - нет.

Наиболее точная симметрия осуществляется в мире кристаллов, но и здесь она неидеальная: невидимые глазом трещинки, царапины всегда делают равные грани слегка отличными друг от друга.

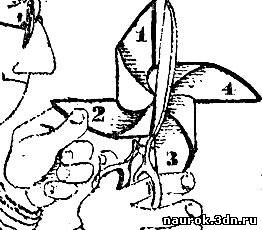
Рис. 2.8

На рис. 2.8 изображена детская бумажная вертушка. Она тоже симметрична, но плоскость симметрии через нее провести нельзя. В чем же тогда заключается симметрия этой фигурки? Прежде всего спросим себя о симметричных ее частях. Сколько их? Очевидно, четыре. В чем заключается правильность взаимного расположения этих одинаковых частей? Это также нетрудно заметить. Повернем вертушку на прямой угол против часовой стрелки, т. е. на ¹/₄ окружности: тогда крыло 1 встанет на то место, где было крыло 2, крыло 2 - на место 3, 3 - на место 4 и 4 - на место 1. Новое положение неотличимо от предыдущего. Про такую фигурку мы скажем так: она обладает осью симметрии, говоря точнее - осью симметрии 4-го порядка, так как совмещение происходит при повороте на ¹/₄ окружности.

Итак, ось симметрии - это такая прямая линия, поворотом около которой на долю оборота можно перевести тело в положение, не отличимое от исходного. Порядок оси (в нашем случае 4-й) указывает, что такое совмещение происходит при повороте на ¹/₄ окружности. Следовательно, четырьмя последовательными поворотами мы возвращаемся в исходное положение.

Встречаемся ли мы с симметрией любого типа в царстве кристаллов? Опыт показывает, что нет.

В кристаллах мы встречаемся лишь с осями симметрии 2-, 3-, 4- и 6-го порядков. И это не случайно. Кристаллографы доказали, что это связано с внутренним строением кристалла. Поэтому число различных видов или, как говорят, классов симметрии кристаллов относительно невелико - оно равно.