Цели урока:
- Образовательная: ввести формулировки и
границы применимости трёх законов движения
планет (законов Кеплера).
- Развивающая: развивать логическое
мышление, правильную речь, использовать
соответствующую терминологию.
- Воспитательная: достигать высокой
активности класса, внимания, сосредоточенности
учащихся на уроке.
Оборудование:
- 2 булавки,
- нитка,
- карандаш.
Эксперимент: чертёж эллипса.
ХОД УРОКА
I. Актуализация знаний
– Здравствуйте, ребята! Садитесь! Сегодня мы с
вами продолжим изучать познание неба и на уроке
познакомимся с тремя законами движения планет и
искусственных тел Солнечной системы. А сейчас
проверим, как вы усвоили материал прошлых
занятий.
II. Проверка домашнего задания
(Каждому ученику по вариантам раздаются
карточки с заданиями)
| 1 вариант |
2 вариант |
| 1. Что изучает астрономия? |
1. Что такое созвездия? |
| 2. Нарисуйте схематично небесную сферу и
математический горизонт и обозначьте все
известные Вам точки на сфере. |
2. Нарисуйте небесную сферу и обозначьте
известные Вам её элементы. |
| 3. День весеннего равноденствия. |
3. День осеннего равноденствия. |
| 4. По новому стилю 25 января 1900 г. Какая это дата
по старому стилю? |
4. По старому стилю – 25 декабря 1899 г. Какая это
дата по новому стилю? |
5. На какую высоту в Москве (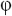 = 56°) поднимается Солнце в полдень
и дни равноденствия? = 56°) поднимается Солнце в полдень
и дни равноденствия? |
5. На какой высоте в Москве (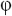 = 56°) проходит верхнюю кульминацию
Денеб ( = 56°) проходит верхнюю кульминацию
Денеб (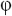 = 45°)? = 45°)? |
III. Объяснение нового теоретического
материала
Заслуга открытия законов движения планет
принадлежит выдающемуся немецкому учёному,
астроному и математику, Иоганну Кеплеру (1571 – 1630
гг.) –
человеку большого мужества и необыкновенной
любви к науке. Он проявил себя ревностным
сторонником системы мира Коперника и задался
целью уточнить строение Солнечной системы. Тогда
это означало: познать законы движения планет,
или, как он выразился, «проследить замысел Бога
при cотворении мира». В начале XVII в. Кеплер,
изучая обращение Марса вокруг Солнца, установил
три закона движения планет.
Первый закон Кеплера
Каждая планета обращается вокруг Солнца по
эллипсу, в одном из фокусов которого находится
Солнце.
или
Под действием силы притяжения одно небесное
тело движется в поле тяготения другого небесного
тела по одному из конических сечений – кругу,
эллипсу, параболе или гиперболе.
Эллипсом называется плоская замкнутая кривая, имеющая
такое свойство, что сумма расстояний каждой её
точки от двух точек, называемых фокусами, остаётся
постоянной. Эта сумма расстояний равна длине
большой оси эллипса. Точка О – центр эллипса, F1
и F2 – фокусы. Солнце находится в данном
случае в фокусе F1.
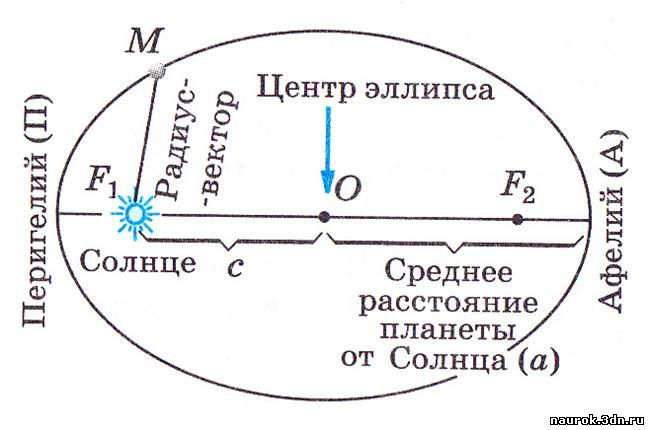
Ближайшая к Солнцу точка орбиты называется перигелием,
самая далёкая – афелием. Линия,
соединяющая какую-либо точку эллипса с фокусом,
называется радиус-вектором. Отношение
расстояния между фокусами к большой оси (к
наибольшему диаметру) называется эксцентриситетом
е. эллипс тем сильнее вытянут, чем
больше его эксцентриситет. Большая полуось
эллипса а – среднее расстояние
планеты до Солнца.
По эллиптическим орбитам движутся и кометы и
астероиды. У окружности е = 0, у
эллипса 0 < е < 1, у параболы е
= 1, у гиперболы е > 1.
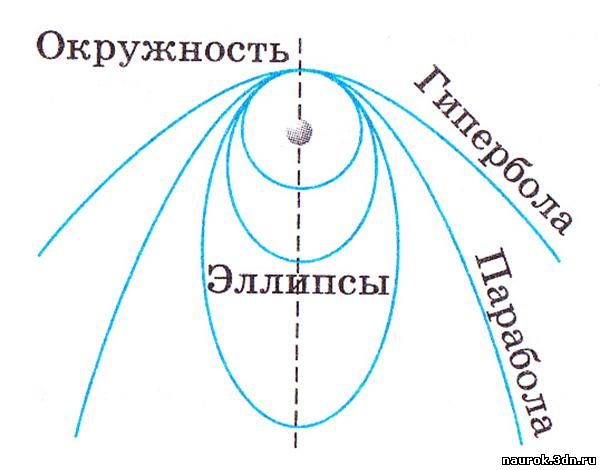
Орбиты планет – эллипсы, мало отличаются от
окружностей; их эксцентриситеты малы. Например,
эксцентриситет орбиты Земли е = 0,017.
Второй закон Кеплера
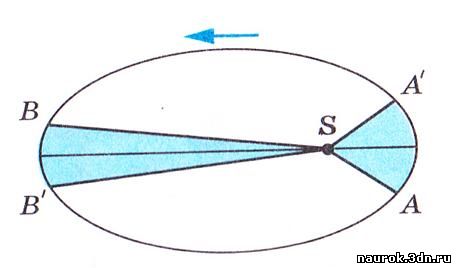
Радиус-вектор планеты за одинаковые
промежутки времени описывает равные площади (определяет
скорость движения планеты по орбите).
Скорость планеты тем больше, чем она ближе к
Солнцу.
Планета проходит путь от точки А до А1 и от В
до В1 за одно и
то же время. Другими словами, планета движется
быстрее всего в перигелии, а медленнее всего –
когда находится на наибольшем удалении (в
афелии). Так, скорость кометы Галлея в перигелии
равна 55 км/с, а в афелии 0,9 км/с.
Самый близкий к Солнцу Меркурий обегает вокруг
светила за 88 дней. За ним движется Венера, и год на
ней длится 225 земных суток. Земля обращается
вокруг Солнца за 365 суток, то есть ровно за один
год. Марсианский год почти в два раза
продолжительнее земного. Юпитерский год равен
почти 12 земным годам, а далёкий Сатурн обходит
свою орбиту за 29,5 лет! Словом, чем дальше
планета от Солнца, тем продолжительнее на
планете год. И Кеплер пытался найти
зависимость между размерами орбит различных
планет и временем их обращения вокруг Солнца.
15 мая 1618 года после множества неудачных попыток
Кеплер установил наконец очень важное
соотношение, известное как
Третий закон Кеплера
Квадраты периодов обращения планет вокруг
Солнца относятся как кубы их средних расстояний
от Солнца.
Если периоды обращения любых двух планет,
например Земли и Марса, обозначить через Тз
и Тм , а их средние расстояния от Солнца – аз
и ам, то третий закон Кеплера можно
записать в виде равенства:
Т2м / Т2з = а3м
/ а3з.
Но ведь период обращения Земли вокруг Солнца
равен одному году (Тз = 1), а среднее
расстояние Земля – Солнце принято за одну
астрономическую единицу (аз = 1 а.е.). Тогда
данное равенство примет более простой вид:
Т2м – а3м
Период обращения планеты (в нашем примере
Марса) можно определить из наблюдений. Он
составляет 687 земных суток, или 1,881 года. Зная это,
нетрудно вычислить среднее расстояние планеты
от Солнца в астрономических единицах:
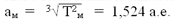
Т.е. Марс находится в среднем в 1,524 раза дальше
от Солнца, чем наша Земля. Следовательно, если
известно время обращения какой-нибудь планеты,
то по нему можно найти её среднее расстояние от
Солнца. Таким путём Кеплеру удалось определить
расстояния всех известных в ту пору планет:
Меркурий – 0,39,
Венера – 0,72,
Земля – 1,00
Марс – 1,52,
Юпитер – 5,20,
Сатурн – 9,54.
Только это были относительные расстояния –
числа, показывающие, во сколько раз та или иная
планета дальше от Солнца или ближе к Солнцу, чем
Земля. Истинные значения этих расстояний,
выраженные в земных мерах (в км), оставались
неизвестными, ибо ещё не была известна длина
астрономической единицы – среднего расстояния
Земли от Солнца.
Третий закон Кеплера связал в единую стройную
систему всё солнечное семейство. На поиски ушло
девять трудных лет. Победило упорство учёного!
Вывод: законы Кеплера теоретически
развивали гелиоцентрическое учение и тем самым
укрепляли позиции новой астрономии. Астрономия
Коперника – самое мудрое из всех произведений
человеческого ума. [1]
Последующие наблюдения показали, что законы
Кеплера применимы не только для планет Солнечной
системы и их спутников, но и для звёзд, физически
связанных между собой и обращающихся вокруг
общего центра масс. Они легли в основу
практической космонавтики, ибо по законам
Кеплера движутся все искусственные небесные
тела, начиная с первого советского спутника и
кончая современными космическими аппаратами. Не
случайно в истории астрономии Иоганна Кеплера
называют «законодателем неба».
IV. Эксперимент
Взять лист плотной белой бумаги и воткнуть в
него две булавки. Теперь между булавками нужно
натянуть с помощью карандаша нитку со связанными
концами и вести карандаш по бумаге – он вычертит
эллипс.
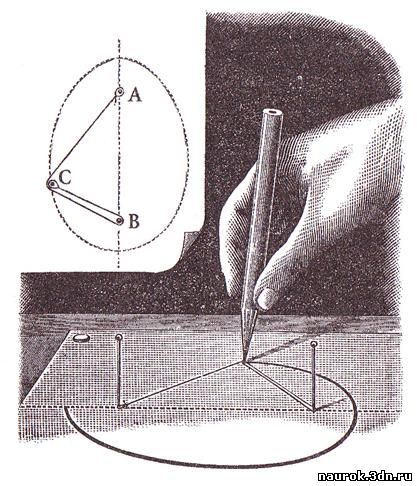
Внутри эллипса
есть две точки (отверстия, проколотые булавками),
обладающие замечательным свойством: сумма двух
линий, соединяющих эти точки с любой точкой
эллипса, всегда одинакова и равна длине большой
оси (т.е. наибольшему диаметру) эллипса. Эти две
точки называются фокусами эллипса, а всякая
прямая линия, соединяющая фокус с любой точкой
эллипса, есть радиус-вектор. Если мы разделим
расстояние между фокусами на длину большой оси,
получим отношение, которое называется эксцентриситетом
данного эллипса. Эксцентриситет характеризует
вытянутость эллипса. Чем большим
эксцентриситетом обладает эллипс, т.е. чем больше
расстояние между фокусами при одной и той же
длине большой оси, тем более он вытянут. При
эксцентриситетом, равном единице, т.е. по
абсолютной величине равном длине большой оси
эллипса, последний превращается в разомкнутую
кривую – параболу. С уменьшением
эксцентриситета вытянутость эллипса, наоборот,
уменьшается, и когда эксцентриситет становится
равным нулю, эллипс превращается в круг.
V. Итог урока
Повторение формулировок первого, второго и
третьего законов Кеплера.
VI. Домашнее задание
|  З В О Н О К НА У Р О К
З В О Н О К НА У Р О К З В О Н О К НА У Р О К
З В О Н О К НА У Р О К